Question

【题目】如图，已知OB是∠AOC的角平分线，OD是∠COE的角平分线，

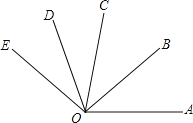
（1）若∠BOE=110°，∠AOB=30°，求∠COE的度数；

（2）若∠AOE=140°，∠AOC=60°，求∠DOE的度数．

Answer 1

【答案】（1）80°；（2）40°．

【解析】

试题分析：（1）由角平分线的定义可知∠BOC=∠AOB，又∠COE=∠BOE﹣∠BOC，易得结果；

（2）由已知易得∠EOC的度数，再利用角平分线的定义可得∠DOE=，可得结果．

解：（1）∵∠AOB=30°，OB是∠AOC的角平分线，∠BOE=110°，

∴∠BOC=∠AOB=30°，

∴∠COE=∠BOE﹣∠BOC=110°﹣30°=80°；

（2）∵∠AOE=140°，∠AOC=60°，

∴∠EOC=∠AOE﹣∠AOC=140°﹣60°=80°，

∵OD是∠COE的角平分线，

∴∠DOE==40°．