题目内容
【题目】如图,∠BAC=120°,AD平分∠BAC,且AD=4,点P是射线AB上一动点,连接DP,△PAD的外接圆于AC交于点Q,则线段QP的最小值是 .

【答案】2![]() .
.
【解析】
试题分析:根据圆周角定理求出∠DQP=∠DPQ=60°,求出△PDQ是等边三角形,推出PQ=DP,求出PD的最小值,即可得出答案.
连接DQ,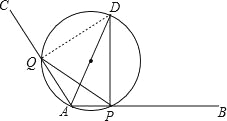
∵∠BAC=120°,AD平分∠BAC, ∴∠CAD=∠DAB=60°, ∴∠DQP=∠DAB=60°,∠DPQ=∠DAC=60°,
∴∠DQP=∠DPQ=60°, ∴△PDQ是等边三角形, ∴DP=PQ, 在△DAP中,由余弦定理得:DP2=AD2+AP2﹣2ADAPcos∠DAP, ∵∠DAP=60°,AD=4, ∴DP2=PA2﹣4PA+16=(PA﹣2)2+12, 即当PA=2时,DP2有最小值12, 即DP=2![]() , ∴PQ的最小值是2
, ∴PQ的最小值是2![]()

练习册系列答案
相关题目