题目内容
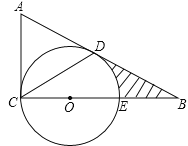
【题目】如图,在△ABE中∠AEB=90°,AB=![]() ,以AB为边在△ABE的同侧作正方形ABCD,点O为AC与BD的交点,连接OE,OE=2
,以AB为边在△ABE的同侧作正方形ABCD,点O为AC与BD的交点,连接OE,OE=2![]() ,点P为AB上一点,将△APE沿直线PE翻折得到△GPE,若PG⊥BE于点F,则BF= .
,点P为AB上一点,将△APE沿直线PE翻折得到△GPE,若PG⊥BE于点F,则BF= .

【答案】5-![]() .
.
【解析】
试题解析:如图,在BE上截取BM=AE,连接OM,OE,AC与BE交于点K,
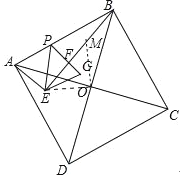
∵四边形ABCD是正方形,
∴AC⊥BD,AO=OB,
∴∠AEB=∠AOB=90°,
∴∠EAK+∠AKE=90°,∠BKO+∠OBM=90°,
∵∠BKO=∠AKE,
∴∠EAO=∠OBM,
在△OAE和△OBM中,
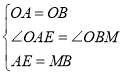 ,
,
∴△OAE≌△OBM,
∴OE=OM,∠AOE=∠BOM,
∴∠EOM=∠AOB=90°,
∴EM=![]() OE=4,设AE=BM=a,
OE=4,设AE=BM=a,
在RT△ABE中,∵AB2=AE2+BE2,
∴26=a2+(a+4)2,
∵a>0,
∴a=1,
∵△PEG是由△PEA翻折,
∴PA=PG,∠APE=∠GPE,
∵PG⊥EB,AE⊥EB,
∴AE∥PG,
∴∠AEP=∠GPE=∠APE,
∴AP=AE=1,PB=![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴BF=5-![]() .
.

练习册系列答案
相关题目