ЬтФПФкШн
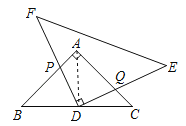
ЁОЬтФПЁПНЋЕШбќжБНЧШ§НЧаЮABCЃЈABЃНACЃЌЁЯBACЃН90ЁуЃЉКЭЕШбќжБНЧШ§НЧаЮDEFЃЈDEЃНDFЃЌЁЯEDFЃН90ЁуЃЉАДЭМ1АкЗХЃЌЕуDдкBCБпЕФжаЕуЩЯЃЌЕуAдкDEЩЯЃЎ

ЃЈ1ЃЉЬюПеЃКABгыEFЕФЮЛжУЙиЯЕЪЧЁЁ ЁЁЃЛ
ЃЈ2ЃЉЁїDEFШЦЕуDАДЫГЪБеыЗНЯђзЊЖЏжСЭМ2ЫљЪОЮЛжУЪБЃЌDFЃЌDEЗжБ№НЛABЃЌACгкЕуPЃЌQЃЌЧѓжЄЃКЁЯBPD+ЁЯDQCЃН180ЁуЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌдкЁїDEFШЦЕуDАДЫГЪБеыЗНЯђзЊЖЏЙ§ГЬжаЃЌЪМжеЕуPВЛЕНДяAЕуЃЌЁїABCЕФУцЛ§МЧЮЊS1ЃЌЫФБпаЮAPDQЕФУцЛ§МЧЮЊS2ЃЌФЧУДS1гыS2жЎМфЪЧЗёДцдкВЛБфЕФЪ§СПЙиЯЕЃПШєДцдкЃЌЧыаДГіЫќУЧжЎМфЕФЪ§СПЙиЯЕВЂжЄУїЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉЦНааЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉДцдкЃЌS1ЃН2S2ЃЌРэгЩМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪКЭЦНааЯпЕФХаЖЈЗНЗЈМДПЩЕУЕННсТлЃЛ
ЃЈ2ЃЉИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪЕУЕНЁЯBЃНЁЯCЃН45ЁуЃЌдйИљОнШ§НЧаЮЕФФкНЧКЭМДПЩЕУЕННсТлЃЛ
ЃЈ3ЃЉСЌНгADЃЌИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪКЭгрНЧЕФаджЪПЩЕУBDЃНCDЃНADЃЌЁЯBЃНЁЯCADЃЌЁЯBDPЃНЁЯADQЃЌНјЖјПЩИљОнASAжЄУїЁїBDPЁеЁїADQЃЌдйИљОнШЋЕШШ§НЧаЮЕФаджЪМДПЩЕУЕННсТлЃЎ
НтЃКЃЈ1ЃЉЁпABЃНACЃЌЁЯBACЃН90ЁуЃЌЁрЁЯABDЃНЁЯC=45ЁуЃЌ
ЁпDEЃНDFЃЌЁЯEDFЃН90ЁуЃЌЁрЁЯFЃНЁЯEЃН45ЁуЃЌ
ЁрЁЯFЃНЁЯ ABDЃЌЁрABЁЮEFЃЛ
ЙЪД№АИЮЊЃКЦНааЃЛ
ЃЈ2ЃЉЁпABЃНACЃЌЁЯBACЃН90ЁуЃЌЁрЁЯBЃНЁЯCЃН45ЁуЃЌ
ЁпЁЯEDFЃН90ЁуЃЌЁрЁЯBDP+ЁЯCDQЃН90ЁуЃЌ
ЁрЁЯBPD+ЁЯDQCЃН360ЁуЉЁЯBЉЁЯCЉЁЯBDPЉЁЯCDQЃН180ЁуЃЛ
ЃЈ3ЃЉS1гыS2жЎМфДцдкВЛБфЕФЪ§СПЙиЯЕЃКS1ЃН2S2.
РэгЩЃКСЌНгADЃЌШчЭМЃЌЁпABЃНACЃЌADЁЭBCЃЌ
ЁрBDЃНCDЃНADЃН![]() BCЃЌЁЯBЃНЁЯCЃНЁЯCADЃН45ЁуЃЌ
BCЃЌЁЯBЃНЁЯCЃНЁЯCADЃН45ЁуЃЌ
ЁпЁЯBDP+ЁЯADPЃНЁЯADP+ЁЯADQЃН90ЁуЃЌ
ЁрЁЯBDPЃНЁЯADQЃЌ
ЁрЁїBDPЁеЁїADQЃЈASAЃЉЃЌ
ЁрSЁїABDЃНSЁїBPD+SЁїAPDЃНSЁїADQ+SЁїAPDЃНS2ЃЌ
гжЁпSЁїADBЃН![]() S1ЃЌ
S1ЃЌ
ЁрS1ЃН2S2ЃЎ