题目内容
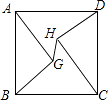
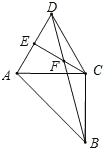
【题目】.如图,以等腰直角△ABC 的直角边 AC 作等边△ACD,CE⊥AD 于 E, BD、CE 交于点 F.
(1)求∠DFE 的度数;
(2)求证:AB=2DF.
【答案】(1)45°;(2)见解析.
【解析】
(1)根据等边三角形的性质可得∠ACD 的大小,根据 BC=CD 即可求得∠CDB,即可求得∠ADB,即可解题;
(2)根据∠DFE=45°可得△DEF 为等腰直角三角形,根据 AD=2DE 即可解题.
(1)∵△ACD 是等边三角形,
∴∠ACD=60°,
∴∠BCD=60°+90°=150°,
∵BC=CD
∴∠BDC= ![]() (180°﹣150°)=15°,
(180°﹣150°)=15°,
∴∠ADF=60°﹣15°=45°,
∴∠DFE=180°﹣∠DEF﹣∠EDF=45°,
(2)∵CE⊥AD,∠DFE= 45°,
∴△DEF 为等腰直角三角形,
∵△ABC 是等腰直角三角形,
∴△ACB∽△DEF,
∴![]() =
=![]() =
=![]() ,
,
∴AB=2DE.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
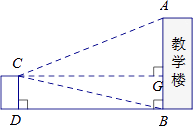
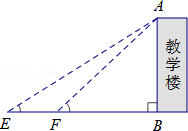
【题目】某校数学课题学习小组在“测量教学楼高度”的活动中,设计了以下两种方案:
课题 | 测量教学楼高度 | |
方案 | 一 | 二 |
图示 |
|
|
测得数据 | CD=6.9m,∠ACG=22°,∠BCG=13°, | EF=10m,∠AEB=32°,∠AFB=43° |
参考数据 | sin22°≈0.37,cos22°≈0.93, | sin32°≈0.53,cos32°≈0.85,tan32°≈0.62 |
请你选择其中的一种方法,求教学楼的高度(结果保留整数)