题目内容
【题目】阅读下面材料：点A、B在数轴上分别表示实数a、b，A，B两点之间的距离表示为│AB│.当A、B两点中有一点在原点时，不妨设点A在原点，如图1，|AB|=|OB|=|b|=|ab|；
当A、B两点都不在原点时，
①如图2,点A、B都在原点的右边,|AB|=|OB||OA|=|b||a|=ba=|ab|；
②如图3,点A、B都在原点的左边,|AB|=|OB||OA|=|b||a|=b(a)=ab=│a-b│；
③如图4,点A、B在原点的两边,|AB|=|OB|+|OA|=|b|+|a|=-b+a=|ab|；综上，数轴上A、B两点之间的距离|AB|=|ab|.
（1）回答下列问题：
①数轴上表示3和9的两点之间的距离是______，数轴上表示5和9的两点之间的距离是______，数轴上表示10和3的两点之间的距离是______；
②数轴上表示x和4的两点A和B之间的距离为______，如果|AB|=6，那么x为______；
③当代数式|x+2|+|x3|取最小值______时，相应的x的取值范围是______.
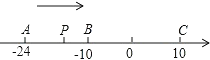
（2）a、b在数轴上位置如图所示，请化简式子│a+1│-│2b-2│-│a+b│
【答案】（1）①6，4，13；②
，2或-10；③5，-2≤x≤3；（2）3b-3.
【解析】
（1）①根据数轴上A、B两点之间的距离|AB|=|ab|即可得答案；②根据数轴上两点间的距离公式解答即可；③|x+2|+|x3|可表示某点到表示-2和3的点的距离的和，可得这一点表示的数在-2和3之间时，|x+2|+|x3|取最小值，根据绝对值的性质化简即可得答案；（2）由数轴可得a<-1，0<b<1，即可判断a+1、2b-2、a+b的符号，根据绝对值的性质化简即可得答案.
（1）①数轴上表示3和9的两点之间的距离是
=6，
数轴上表示5和9的两点之间的距离是
=4，
数轴上表示10和3的两点之间的距离是
=13，
故答案为：6，4，13
②数轴上表示x和4的两点A和B之间的距离为
=，
∵=6，
∴x+4=6或x+4=-6，
∴x=2或x=-10，
故答案为：，2或-10
③∵代数式|x+2|+|x-3|可看作数轴上某点到表示-2和3的点的距离之和，
∴当该点表示的数在-2和3之间时，|x+1|+|x+2|取最小值．
∴-2≤x≤3．
∴x+2≥0，x-3≤0，
∴|x+2|+|x-3|=x+2-(x-3)=x+2-x+3=5
∴当代数式|x+2|+|x3|取最小值5时，相应的x的取值范围是-2≤x≤3．
故答案为：5，-2≤x≤3
（2）由数轴可知a<-1，0<b<1，
∴a+1<0，b-1<0，a+b<0，
∴│a+1│-│2b-2│-│a+b│
=-(a+1)+(2b-2)+(a+b)
=3b-3.
