ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§A(aΘ§0)Θ§C(0Θ§c)«“¬ζΉψΘΚ(a+6)2+![]() ΘΫ0Θ§≥ΛΖΫ–ΈABCO‘ΎΉχ±ξœΒ÷–(»γΆΦ)Θ§ΒψOΈΣΉχ±ξœΒΒΡ‘≠ΒψΘ°
ΘΫ0Θ§≥ΛΖΫ–ΈABCO‘ΎΉχ±ξœΒ÷–(»γΆΦ)Θ§ΒψOΈΣΉχ±ξœΒΒΡ‘≠ΒψΘ°

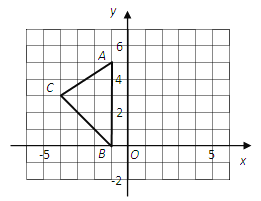
(1)«σΒψBΒΡΉχ±ξΘ°
(2)»γΆΦ1Θ§»τΒψM¥”ΒψA≥ωΖΔΘ§“‘2ΗωΒΞΈΜ/ΟκΒΡΥΌΕ»œρ”“‘ΥΕ·(≤Μ≥§ΙΐΒψO)Θ§ΒψN¥”‘≠ΒψO≥ωΖΔΘ§“‘1ΗωΒΞΈΜ/ΟκΒΡΥΌΕ»œρœ¬‘ΥΕ·(≤Μ≥§ΙΐΒψC)Θ§…ηMΓΔNΝΫΒψΆ§ ±≥ωΖΔΘ§‘ΎΥϋΟ«‘ΥΕ·ΒΡΙΐ≥Χ÷–Θ§ΥΡ±Ώ–ΈMBNOΒΡΟφΜΐ «ΖώΖΔ…ζ±δΜ·ΘΩ»τ≤Μ±δΘ§«σΤδ÷ΒΘΜ»τ±δΜ·Θ§«σ±δΜ·ΒΡΖΕΈßΘ°
(3)»γΆΦ2Θ§EΈΣx÷αΗΚΑκ÷α…œ“ΜΒψΘ§«“ΓœCBEΘΫΓœCEBΘ§F «x÷α’ΐΑκ÷α…œ“ΜΕ·ΒψΘ§ΓœECFΒΡΤΫΖ÷œΏCDΫΜBEΒΡ―”≥ΛœΏ”ΎΒψDΘ§‘ΎΒψF‘ΥΕ·ΒΡΙΐ≥Χ÷–Θ§«κΧΫΨΩΓœCFE”κΓœDΒΡ ΐΝΩΙΊœΒΘ§≤ΔΥΒΟςάμ”…
ΓΨ¥πΑΗΓΩ(1)B(©¹6Θ§©¹3)ΘΜ(2)ΥΡ±Ώ–ΈMBNOΒΡΟφΜΐ≤Μ±δΘΜ «Ε®÷Β9ΘΜ(3)ΓœCFEΘΫ2ΓœD.
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΧβ“βΩ…ΒΟaΘΫ©¹6Θ§cΘΫ©¹3Θ§‘ρΩ…«σAΒψΘ§CΒψΘ§BΒψΉχ±ξΘΜΘ®2Θ©…ηMΓΔNΆ§ ±≥ωΖΔΒΡ ±ΦδΈΣtΘ§‘ρSΥΡ±Ώ–ΈMBNOΘΫS≥ΛΖΫ–ΈOABC©¹SΓςABM©¹SΓςBCNΘΫ18©¹![]() ΓΝ2tΓΝ3©¹
ΓΝ2tΓΝ3©¹![]() ΓΝ6ΓΝΘ®3©¹tΘ©ΘΫ9Θ°”κ ±ΦδΈόΙΊΘ°Φ¥ΟφΜΐ «Ε®÷ΒΘ§Τδ÷ΒΈΣ9ΘΜΘ®3Θ©ΗυΨί»ΐΫ«–ΈΡΎΫ«ΚΆΕ®άμΚΆ»ΐΫ«–ΈΆβΫ«Β»”Ύ≤ΜœύΝΎΒΡΝΫΗωΡΎΫ«ΒΡΚΆΘ§Ω…«σΓœCFE”κΓœDΒΡ ΐΝΩΙΊœΒΘ°
ΓΝ6ΓΝΘ®3©¹tΘ©ΘΫ9Θ°”κ ±ΦδΈόΙΊΘ°Φ¥ΟφΜΐ «Ε®÷ΒΘ§Τδ÷ΒΈΣ9ΘΜΘ®3Θ©ΗυΨί»ΐΫ«–ΈΡΎΫ«ΚΆΕ®άμΚΆ»ΐΫ«–ΈΆβΫ«Β»”Ύ≤ΜœύΝΎΒΡΝΫΗωΡΎΫ«ΒΡΚΆΘ§Ω…«σΓœCFE”κΓœDΒΡ ΐΝΩΙΊœΒΘ°
ΫβΘΚ(1)ΓΏ(a+6)2+![]() ΘΫ0Θ§
ΘΫ0Θ§
ΓύaΘΫ©¹6Θ§cΘΫ©¹3
ΓύA(©¹6Θ§0)Θ§C(0Θ§©¹3)
ΓΏΥΡ±Ώ–ΈOABC «ΨΊ–Έ
ΓύAOΓΈBCΘ§ABΓΈOCΘ§ABΘΫOCΘΫ3Θ§AOΘΫBCΘΫ6
ΓύB(©¹6Θ§©¹3)
(2)ΥΡ±Ώ–ΈMBNOΒΡΟφΜΐ≤Μ±δΘ°
…ηMΓΔNΆ§ ±≥ωΖΔΒΡ ±ΦδΈΣtΘ§
‘ρSΥΡ±Ώ–ΈMBNOΘΫS≥ΛΖΫ–ΈOABC©¹SΓςABM©¹SΓςBCNΘΫ18©¹![]() ΓΝ2tΓΝ3©¹
ΓΝ2tΓΝ3©¹![]() ΓΝ6ΓΝ(3©¹t)ΘΫ9Θ°”κ ±ΦδΈόΙΊΘ°
ΓΝ6ΓΝ(3©¹t)ΘΫ9Θ°”κ ±ΦδΈόΙΊΘ°
Γύ‘Ύ‘ΥΕ·Ιΐ≥Χ÷–ΟφΜΐ≤Μ±δΘ° «Ε®÷Β9
(3)ΓœCFEΘΫ2ΓœDΘ°
άμ”…»γœ¬ΘΚ»γΆΦ
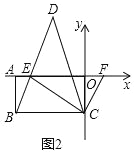
ΓΏΓœCBEΘΫΓœCEB
ΓύΓœECBΘΫ180Γψ©¹2ΓœBEC
ΓΏCDΤΫΖ÷ΓœECF
ΓύΓœDCEΘΫΓœDCF
ΓΏAFΓΈBC
ΓύΓœFΘΫ180Γψ©¹ΓœDCF©¹ΓœDCE©¹ΓœBCEΘΫ180Γψ©¹2ΓœDCE©¹(180Γψ©¹2ΓœBEC)
ΓύΓœFΘΫ2ΓœBEC©¹2ΓœDCE
ΓΏΓœBECΘΫΓœD+ΓœDCE
ΓύΓœFΘΫ2(ΓœD+ΓœDCE)©¹2ΓœDCE
ΓύΓœFΘΫ2ΓœD