题目内容
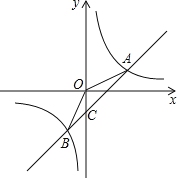
【题目】如图,已知反比例函数的图象![]() 与一次函数
与一次函数![]() 的图象交于
的图象交于![]() 两点,且
两点,且![]() .
.
(1)求反比例函数和一次函数的关系式;
(2)利用图象直接写出当![]() 在什么范围时,
在什么范围时, ![]() ;
;
(3)求出三角形AOB的面积.

【答案】(1)![]()
![]() (2)
(2)![]() 或
或![]() (3)
(3)![]()
【解析】试题分析:(1)将点A(2,n),B(﹣1,﹣2)代入反比例函数y1=![]() 中得:2n=(﹣1)×(﹣2)=k1,可求k1、n;再将点A(2,n),B(﹣1,﹣2)代入y2=k2x+b中,列方程组求k2、b即可;
中得:2n=(﹣1)×(﹣2)=k1,可求k1、n;再将点A(2,n),B(﹣1,﹣2)代入y2=k2x+b中,列方程组求k2、b即可;
(2)根据两函数图象的交点,图象的位置可确定y1>y2时x的范围;
(3)要求△AOB的面积,可以分两部分求解.首先根据直线AB的解析式求得与y轴的交点坐标,进一步根据y轴所分成的两个三角形的面积求解.
试题解析:解:(1)∵双曲线y1=![]() 过点(﹣1,﹣2),∴k1=﹣1×(﹣2)=2.
过点(﹣1,﹣2),∴k1=﹣1×(﹣2)=2.
∵双曲线y1=![]() ,过点(2,n),∴n=1.
,过点(2,n),∴n=1.
由直线y2=k2x+b过点A,B得:
![]() ,解得
,解得![]() ,∴反比例函数关系式为y1=
,∴反比例函数关系式为y1=![]() ,一次函数关系式为y2=x﹣1.
,一次函数关系式为y2=x﹣1.
(2)根据图象得出:当x<﹣1或0<x<2时,y1>y2.
(3)由一次函数的解析式,得直线AB与y轴的交点是(0,﹣1),则△AOB的面积=S△BCO+S△ACO=![]() ×1×1+
×1×1+![]() ×1×2=
×1×2=![]() .
.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
【题目】甲、乙两位同学参加数学综合素质测试,各项成绩如下(单位:分)
数与代数 | 空间与图形 | 统计与概率 | 综合与实践 | |
学生甲 | 90 | 93 | 89 | 90 |
学生乙 | 94 | 92 | 94 | 86 |
(1)分别计算甲、乙成绩的中位数;
(2)如果数与代数、空间与图形、统计与概率、综合与实践的成绩按3:3:2:2计算,那么甲、乙的数学综合素质成绩分别为多少分?


