题目内容
(2008•大庆)如图,将非等腰△ABC的纸片沿DE折叠后,使点A落在BC边上的点F处.若点D为AB边的中点,则下列结论:①△BDF是等腰三角形;②∠DFE=∠CFE;③DE是△ABC的中位线,成立的有( )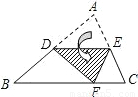
A.①②
B.①③
C.②③
D.①②③
【答案】分析:根据图形可知△DFE是△ADE对折而成,所以两三角形全等,可得AD=DF,而D是AB中点,故有BD=DF,那么①可证;再利用∠ADF是△BDF的外角,可证∠DFB=∠EDF,那么DE∥BC,即DE是△ABC的中位线,②得证;利用DE∥BC,以及△DFE和△ADE的对折,可得∠EFC=∠ECF,即△EFC也是等腰三角形,而∠B≠∠C,即∠DFB,∠DFE,∠EFC,不会同时为60°,那么∠DFE≠∠CFE,故②不成立.
解答:解:由于△DFE是△ADE对折而成,故△DFE≌△ADE,
∴AD=FD,
又∵点D为AB边的中点,
∴AD=BD,
∴BD=DF,即△BDF是等腰三角形,故(1)正确;
由于△DFE是△ADE对折而成,故△DFE≌△ADE,
∴∠ADE=∠FDE,
∵∠ADF=2∠FDE=∠B+∠DFB=2∠DFB,
∴∠FDE=∠DFB,
∴DE∥BC,点E也是AC的中点,故(3)正确;
同理可得△EFC也为等腰三角形,∠C=∠EFC,由于△ABC是非等腰的,
∴∠C≠∠B,也即∠EFC≠∠DFB,
∴∠EFC与∠DFB,∠DFE不都等于60°,
∴②∠DFE=∠CFE就不成立.
故选B.
点评:本题利用了:1、全等的概念,对折后能重合的图形是全等的图形,2、全等三角形的性质,对应角相等,3、内错角相等,两直线平行.
解答:解:由于△DFE是△ADE对折而成,故△DFE≌△ADE,
∴AD=FD,
又∵点D为AB边的中点,
∴AD=BD,
∴BD=DF,即△BDF是等腰三角形,故(1)正确;
由于△DFE是△ADE对折而成,故△DFE≌△ADE,
∴∠ADE=∠FDE,
∵∠ADF=2∠FDE=∠B+∠DFB=2∠DFB,
∴∠FDE=∠DFB,
∴DE∥BC,点E也是AC的中点,故(3)正确;
同理可得△EFC也为等腰三角形,∠C=∠EFC,由于△ABC是非等腰的,
∴∠C≠∠B,也即∠EFC≠∠DFB,
∴∠EFC与∠DFB,∠DFE不都等于60°,
∴②∠DFE=∠CFE就不成立.
故选B.
点评:本题利用了:1、全等的概念,对折后能重合的图形是全等的图形,2、全等三角形的性质,对应角相等,3、内错角相等,两直线平行.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
 m的游船刚好能从桥洞下通过,则这艘游船的最大宽度是多少米?
m的游船刚好能从桥洞下通过,则这艘游船的最大宽度是多少米?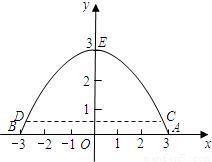
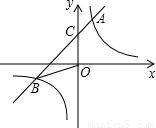
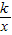 的图象与一次函数y=mx+b的图象相交于两点A(1,3),B(n,-1).
的图象与一次函数y=mx+b的图象相交于两点A(1,3),B(n,-1).
 m的游船刚好能从桥洞下通过,则这艘游船的最大宽度是多少米?
m的游船刚好能从桥洞下通过,则这艘游船的最大宽度是多少米?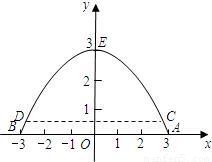
 的图象与一次函数y=mx+b的图象相交于两点A(1,3),B(n,-1).
的图象与一次函数y=mx+b的图象相交于两点A(1,3),B(n,-1).