题目内容
（2008•大庆）如图，河上有一座抛物线桥洞，已知桥下的水面离桥拱顶部3m时，水面宽AB为6m，当水位上升0.5m时：（1）求水面的宽度CD为多少米？
（2）有一艘游船，它的左右两边缘最宽处有一个长方体形状的遮阳棚，此船正对着桥洞在上述河流中航行．
①若游船宽（指船的最大宽度）为2m，从水面到棚顶的高度为1.8m，问这艘游船能否从桥洞下通过？
②若从水面到棚顶的高度为
m的游船刚好能从桥洞下通过，则这艘游船的最大宽度是多少米？
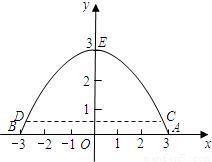
【答案】分析：（1）根据二次函数的对称性，CD=C点横坐标的两倍，由C点纵坐标为0.5所以需先求解析式后再求对应的横坐标；
（2）若船宽2米，根据对称性，对应图象上的点的横坐标为1，代入关系式求纵坐标即为距离水面的高度，与1.8比较后得出结论；由题意知最大宽度为第一象限对应点的横坐标的2倍．
解答：解：（1）设抛物线形桥洞的函数关系式为y=ax2+c，
∵点A（3，0）和E（0，3）在函数图象上
∴
∴
∴
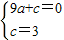
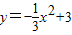
由题意可知，点C和点D的纵坐标为0.5
∴
∴
，
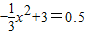
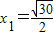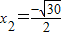
∴CD=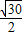
+
=
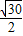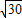（米）；
（2）①当x=1时，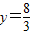
∵
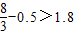
∴这艘游船能从桥洞下通过
②当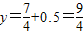
时，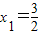
，
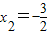（不合题意，舍去）．
∴这艘游船的最大宽度是3米．
点评：根据图象的对称性解题是本题的核心．
（2）若船宽2米，根据对称性，对应图象上的点的横坐标为1，代入关系式求纵坐标即为距离水面的高度，与1.8比较后得出结论；由题意知最大宽度为第一象限对应点的横坐标的2倍．
解答：解：（1）设抛物线形桥洞的函数关系式为y=ax2+c，
∵点A（3，0）和E（0，3）在函数图象上
∴
∴
∴
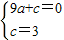
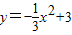
由题意可知，点C和点D的纵坐标为0.5
∴
∴
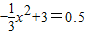
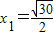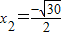
，∴CD=
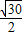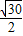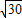+=（米）；（2）①当x=1时，
∵
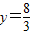
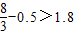
∴这艘游船能从桥洞下通过
②当
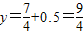时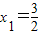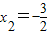，，（不合题意，舍去）．∴这艘游船的最大宽度是3米．
点评：根据图象的对称性解题是本题的核心．
练习册系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案
相关题目
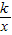的图象与一次函数y=mx+b的图象相交于两点A（1，3），B（n，-1）．
m的游船刚好能从桥洞下通过，则这艘游船的最大宽度是多少米？
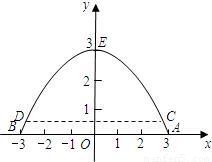
的图象与一次函数y=mx+b的图象相交于两点A（1，3），B（n，-1）．
