题目内容
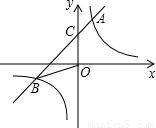
(2008•大庆)如图,反比例函数y= 的图象与一次函数y=mx+b的图象相交于两点A(1,3),B(n,-1).
的图象与一次函数y=mx+b的图象相交于两点A(1,3),B(n,-1).(1)分别求出反比例函数与一次函数的函数关系式;
(2)若直线AB与y轴交于点C,求△BOC的面积.
【答案】分析:(1)根据待定系数法就可以求出函数的解析式;
(2)求△BOC的面积就是求B,C两点的坐标.
解答:解:(1)∵点A(1,3)在反比例函数图象上
∴k=3
即反比例函数关系式为y=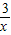
∵点B(n,-1)在反比例函数图象上
∴n=-3
∵点A(1,3)和B(-3,-1)在一次函数y=mx+b的图象上
∴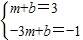
解得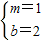
∴一次函数关系式为y=x+2
(2)当x=0时,一次函数值为2
∴OC=2
∴S△BOC= ×2×|-3|=3.
×2×|-3|=3.
点评:用待定系数法确定函数的解析式,是常用的一种解题方法.同学们要熟练掌握这种方法.
(2)求△BOC的面积就是求B,C两点的坐标.
解答:解:(1)∵点A(1,3)在反比例函数图象上
∴k=3
即反比例函数关系式为y=
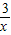
∵点B(n,-1)在反比例函数图象上
∴n=-3
∵点A(1,3)和B(-3,-1)在一次函数y=mx+b的图象上
∴
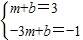
解得
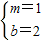
∴一次函数关系式为y=x+2
(2)当x=0时,一次函数值为2
∴OC=2
∴S△BOC=
 ×2×|-3|=3.
×2×|-3|=3.点评:用待定系数法确定函数的解析式,是常用的一种解题方法.同学们要熟练掌握这种方法.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 m的游船刚好能从桥洞下通过,则这艘游船的最大宽度是多少米?
m的游船刚好能从桥洞下通过,则这艘游船的最大宽度是多少米?
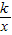 的图象与一次函数y=mx+b的图象相交于两点A(1,3),B(n,-1).
的图象与一次函数y=mx+b的图象相交于两点A(1,3),B(n,-1).
 m的游船刚好能从桥洞下通过,则这艘游船的最大宽度是多少米?
m的游船刚好能从桥洞下通过,则这艘游船的最大宽度是多少米?