题目内容
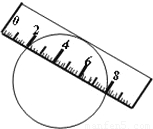
 如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm)则该圆的半径为
如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm)则该圆的半径为
- A.
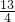 cm
cm - B.3 cm
- C.4 cm
- D.5 cm
A
分析:设OB=rcm,由于刻度尺的宽为2cm,所以OC=r-2,再根据另一边与圆两个交点处的读数恰好为“2”和“8”可求出BC的长,在Rt△OBC中利用勾股定理即可得出r的值.
解答: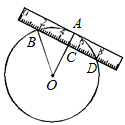 解:设OB=rcm,
解:设OB=rcm,
∵刻度尺的宽为2cm,
∴OC=r-2,
∵另一边与圆两个交点处的读数恰好为“2”和“8”,
∴BC= ×BD=
×BD= ×6=3,
×6=3,
在Rt△OBC中,
∵OB2=OC2+BC2,即r2=(r-2)2+32,解得r=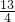 cm.
cm.
故选A.
点评:本题考查的是垂径定理的应用及勾股定理,根据题意得出BC=3是解答此题的关键.
分析:设OB=rcm,由于刻度尺的宽为2cm,所以OC=r-2,再根据另一边与圆两个交点处的读数恰好为“2”和“8”可求出BC的长,在Rt△OBC中利用勾股定理即可得出r的值.
解答:
 解:设OB=rcm,
解:设OB=rcm,∵刻度尺的宽为2cm,
∴OC=r-2,
∵另一边与圆两个交点处的读数恰好为“2”和“8”,
∴BC=
 ×BD=
×BD= ×6=3,
×6=3,在Rt△OBC中,
∵OB2=OC2+BC2,即r2=(r-2)2+32,解得r=
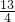 cm.
cm.故选A.
点评:本题考查的是垂径定理的应用及勾股定理,根据题意得出BC=3是解答此题的关键.

练习册系列答案
相关题目
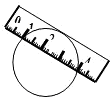 如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“1”和“4”(单位:cm),则该圆的半径为( )
如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“1”和“4”(单位:cm),则该圆的半径为( )| A、5cm | ||
B、(
| ||
C、
| ||
D、
|
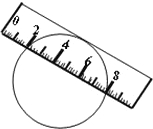 如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm),则该圆的半径为
如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm),则该圆的半径为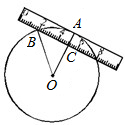 (2012•青岛模拟)如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm)则该圆的半径为( )
(2012•青岛模拟)如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm)则该圆的半径为( ) cm B、
cm B、 cm C、3cm
D、
cm C、3cm
D、 cm
cm