题目内容
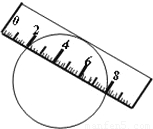
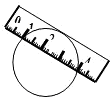 如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“1”和“4”(单位:cm),则该圆的半径为( )
如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“1”和“4”(单位:cm),则该圆的半径为( )| A、5cm | ||
B、(
| ||
C、
| ||
D、
|
分析:根据题意可知,圆内的弦长为3cm,作出弦的弦心距,根据垂径定理和勾股定理,可以求出圆的半径.
解答: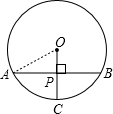 解:如图示,连接OA,根据题意知,
解:如图示,连接OA,根据题意知,
PC=2cm,OP⊥AB,
∴AP=BP,
∵AB=3cm,
∴AP=
cm,
在Rt△AOP中,设OA=x,则0P=x-2,
根据勾股定理得,(
)2+(x-2)2=x2,
解得,x=
.
故选C.
 解:如图示,连接OA,根据题意知,
解:如图示,连接OA,根据题意知,PC=2cm,OP⊥AB,
∴AP=BP,
∵AB=3cm,
∴AP=
| 3 |
| 2 |
在Rt△AOP中,设OA=x,则0P=x-2,
根据勾股定理得,(
| 3 |
| 2 |
解得,x=
| 25 |
| 16 |
故选C.
点评:解决与弦有关的问题时,往往需构造以半径、弦心距和弦长的一半为三边的直角三角形,若设圆的半径为r,弦长为a,这条弦的弦心距为d,则有等式r2=d2+(
)2成立,知道这三个量中的任意两个,就可以求出另外一个.
| a |
| 2 |

练习册系列答案
相关题目
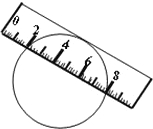 如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm),则该圆的半径为
如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm),则该圆的半径为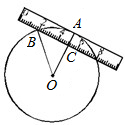 (2012•青岛模拟)如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm)则该圆的半径为( )
(2012•青岛模拟)如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm)则该圆的半径为( ) cm B、
cm B、 cm C、3cm
D、
cm C、3cm
D、 cm
cm