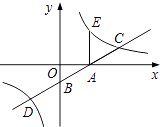Question

【题目】如图，二次函数y=x2+px+q（p＜0）的图象与x轴交于A、B两点，与y轴交于点C（0，﹣1），△ABC的面积为 ．

（1）求该二次函数的关系式；
（2）过y轴上的一点M（0，m）作y轴的垂线，若该垂线与△ABC的外接圆有公共点，求m的取值范围；
（3）在该二次函数的图象上是否存在点D，使四边形ACBD为直角梯形？若存在，求出点D的坐标；若不存在，请说明理由．

Answer 1

【答案】
（1）

解：∵OC=1，

∴q=﹣1，

∵△ABC的面积为 ．

∴ OC×AB= ，

解得AB= ，

设A（a，0），B（b，0），

则a、b是一元二次方程x2+px﹣1=0两个根，

∴a+b=﹣p，ab=﹣1，

∴AB=b﹣a= = ，

解得p= ，

又∵p＜0，

∴p= ．

所以解析式为：y=x2﹣ x﹣1；

（2）

解：如图1所示，

令y=0，

解方程得x2﹣ x﹣1=0，

得x1=﹣ ，x2=2，

所以A（ ，0），B（2，0），

在直角三角形AOC中可求得AC= ，同样可求得BC= ，

显然AC2+BC2=AB2，得三角形ABC是直角三角形．AB为斜边，

所以外接圆的直径为AB= ，

所以 ．

（3）

存在，AC⊥BC，

如图2所示，

①若以AC为底边，则BD∥AC，易求AC的解析式为y=﹣2x﹣1，

可设BD的解析式为y=﹣2x+b，

把B（2，0）代入得BD解析式为y=﹣2x+4，

解方程组

得D（ ，9）

②若以BC为底边，则BC∥AD，易求BC的解析式为y=0.5x﹣1，

可设AD的解析式为y=0.5x+b，把A（ ，0）代入

得AD解析式为y=0.5x+0.25，

解方程组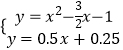

得D（ ）

综上，所以存在两点：（ ，9）或（ ）．

【解析】（1）由△ABC的面积为 ，可得AB×OC= ，又二次函数y=x2+px+q（p＜0）的图象与x轴交于A、B两点，与y轴交于点C（0，﹣1）可求得该二次函数的关系式；（2）根据直线与圆的位置的位置关系确定m的取值范围．（3）四边形ABCD为直角梯形，要分类讨论，即究竟那条边为底．可以分别以AC、BC为底进行讨论．
【考点精析】解答此题的关键在于理解三角形的外接圆与外心的相关知识，掌握过三角形的三个顶点的圆叫做三角形的外接圆，其圆心叫做三角形的外心．