题目内容
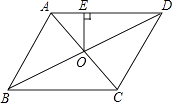
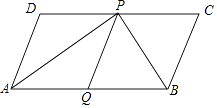
【题目】如图,在ABCD中,AP和BP分别平分∠DAB和∠CBA,PQ∥AD,若AD=5cm,AP=8cm,则△ABP的面积等于cm2 . 
【答案】24
【解析】解:∵四边形ABCD是平行四边形,
∴AD∥CB,AB∥CD,
∴∠DAB+∠CBA=180°,
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB+∠PBA= ![]() (∠DAB+∠CBA)=90°,
(∠DAB+∠CBA)=90°,
在△APB中,∠APB=180°﹣(∠PAB+∠PBA)=90°;
∵AP平分∠DAB,
∴∠DAP=∠PAB,
∵AB∥CD,
∴∠PAB=∠DPA
∴∠DAP=∠DPA
∴△ADP是等腰三角形,
∴AD=DP=5,
同理:PC=CB=5,
即AB=DC=DP+PC=10,
在Rt△APB中,AB=10,AP=8,
∴BP= ![]() =6,
=6,
∴△ABP的面积为: ![]() ×6×8=24(cm2).
×6×8=24(cm2).
所以答案是:24.
【考点精析】本题主要考查了平行四边形的性质的相关知识点,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分才能正确解答此题.

练习册系列答案
相关题目