题目内容
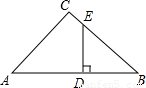
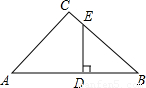
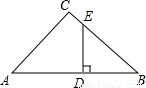
 如图,在面积为75cm2的锐角△ABC中,BC=15cm,从这张硬纸片上剪下一个正方形DEFG,使它的一边EF在BC上,顶点D、G分别在AB,AC上.求这个正方形的边长?
如图,在面积为75cm2的锐角△ABC中,BC=15cm,从这张硬纸片上剪下一个正方形DEFG,使它的一边EF在BC上,顶点D、G分别在AB,AC上.求这个正方形的边长?分析:过点A作AH⊥BC于点H,交DG于点M,先根据△ABC的面积为75cm2,BC=15cm求出AH的长,设这个正方形的边长为x,则MH=x,AM=AD-MH=AD-x,再根据DG∥BC可得出△ADG∽△ABC,根据相似三角形的性质即可得出结论.
解答: 解:过点A作AH⊥BC于点H,交DG于点M,
解:过点A作AH⊥BC于点H,交DG于点M,
∵△ABC的面积为75cm2,BC=15cm,
∴
BC•AH=75,即
×15AH=75,解得AH=10cm,
设这个正方形的边长为x,则MH=x,AM=AH-MH=AH-x=10-x,
∵DG∥BC,
∴△ADG∽△ABC,
∴
=
,即
=
,解得x=6cm.
答:这个正方形的边长为6cm.
 解:过点A作AH⊥BC于点H,交DG于点M,
解:过点A作AH⊥BC于点H,交DG于点M,∵△ABC的面积为75cm2,BC=15cm,
∴
| 1 |
| 2 |
| 1 |
| 2 |
设这个正方形的边长为x,则MH=x,AM=AH-MH=AH-x=10-x,
∵DG∥BC,
∴△ADG∽△ABC,
∴
| DG |
| BC |
| AM |
| AH |
| x |
| 15 |
| 10-x |
| 10 |
答:这个正方形的边长为6cm.
点评:本题考查的是相似三角形的判定和性质、正方形的性质和平行线分线段成比例定理,是各地中考考查相似三角形常见题型.

练习册系列答案
相关题目
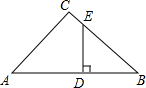 如图,在Rt△ABC中,∠C=90°,DE⊥AB,AC=BE=15,BC=20.则四边形ACED的面积为( )
如图,在Rt△ABC中,∠C=90°,DE⊥AB,AC=BE=15,BC=20.则四边形ACED的面积为( )| A、54 | B、75 | C、90 | D、96 |