题目内容
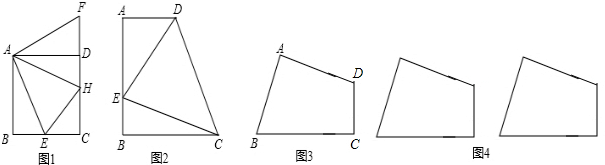
 如图,E在正方形ABCD的边BC延长线上,若CE=AC,AE交D于点F,则∠E=________若AB=2cm,则S△ABE________cm2.
如图,E在正方形ABCD的边BC延长线上,若CE=AC,AE交D于点F,则∠E=________若AB=2cm,则S△ABE________cm2.
22.5°  +2
+2
分析:(1)AC为∠BCD的角平分线,即∠ACE=90°+45°=135°,且根据AC=CE判定△ACE为等腰三角形,即∠E=∠CAF,
(2)已知AB,可以求出对角线AC的长,即CE的长,根据AB,BE可以求△ABE的面积.
解答:(1)AC为正方形ABCD的对角线,
∠ACD=45°,即∠ACE=90°+45°=135°,
∵AC=CE,即∠E=∠CAF,
∴∠E=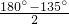 =22.5°;
=22.5°;
(2)AB=2cm,则AC= AB=
AB= cm,
cm,
∴CE=2 cm,
cm,
∴S△ACE= AB×BE=
AB×BE= ×2(2
×2(2 +2)cm2=(2
+2)cm2=(2 +2)cm2,
+2)cm2,
故答案为:22.5°,2 +2.
+2.
点评:本题考查了勾股定理在直角三角形中的运用,等腰三角形的判定,等腰三角形腰长相等的性质,三角形面积的计算,正确的计算AC的长是解题的关键.
 +2
+2分析:(1)AC为∠BCD的角平分线,即∠ACE=90°+45°=135°,且根据AC=CE判定△ACE为等腰三角形,即∠E=∠CAF,
(2)已知AB,可以求出对角线AC的长,即CE的长,根据AB,BE可以求△ABE的面积.
解答:(1)AC为正方形ABCD的对角线,
∠ACD=45°,即∠ACE=90°+45°=135°,
∵AC=CE,即∠E=∠CAF,
∴∠E=
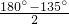 =22.5°;
=22.5°;(2)AB=2cm,则AC=
 AB=
AB= cm,
cm,∴CE=2
 cm,
cm,∴S△ACE=
 AB×BE=
AB×BE= ×2(2
×2(2 +2)cm2=(2
+2)cm2=(2 +2)cm2,
+2)cm2,故答案为:22.5°,2
 +2.
+2.点评:本题考查了勾股定理在直角三角形中的运用,等腰三角形的判定,等腰三角形腰长相等的性质,三角形面积的计算,正确的计算AC的长是解题的关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目

 构造一个与上述命题类似的正确命题并加以证明.
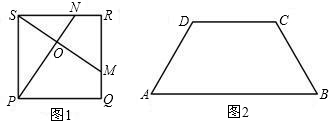
构造一个与上述命题类似的正确命题并加以证明. 26、如图1,在正方形ABCD中,若点E是△DBC内的一点,且DE=DC,BE=CE.
26、如图1,在正方形ABCD中,若点E是△DBC内的一点,且DE=DC,BE=CE.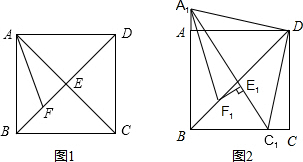 如图1,在正方形ABCD中,对角线AC与BD相交于点E,AF平分∠BAC,交BD于点F.
如图1,在正方形ABCD中,对角线AC与BD相交于点E,AF平分∠BAC,交BD于点F.