题目内容
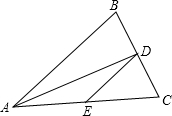
如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为

| A.20 | B.18 | C.14 | D.13 |
C
试题分析:∵AB=AC,AD平分∠BAC,BC=8,
∴根据等腰三角形三线合一的性质得:AD⊥BC,CD=BD=
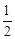 BC=4。
BC=4。∵点E为AC的中点,
∴根据直角三角形斜边上的中线等于斜边的一半得:DE=CE=
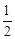 AC=5。
AC=5。∴△CDE的周长=CD+DE+CE=4+5+5=14。故选C。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

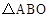 与
与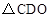 关于O点中心对称,点E、F在线段AC上,且AF=CE。
关于O点中心对称,点E、F在线段AC上,且AF=CE。