��Ŀ����
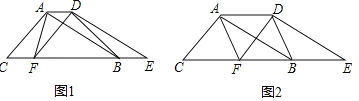
����Ŀ����ͼ������ȫ�ȵġ�ABC�͡�DEF�ص���һ�𣬹̶���ABC������DEF�������±任��
��1����ͼ1����DEF��ֱ��CB����ƽ�ƣ�����F���߶�CB���ƶ���������AF��AD��BD����ֱ��д��S��ABC��S�ı���AFBD�Ĺ�ϵ
��2����ͼ2������Fƽ�Ƶ��߶�BC���е�ʱ�����ı���AFBDΪ�����Σ���ô��ABCӦ����ʲô�����������֤����
��3���ڣ�2���������£�����DEF��DF�۵�����E����FA���ӳ����ϵĵ�G��������CG�����㻭��ͼ�Σ���ʱCG��CF�к�������ϵ��
���𰸡���1��S��ABC=S�ı���AFBD����2���ı���AFBDΪ�����Σ���3��CG=![]() CF��
CF��
��������
�����������1������ƽ���ߵ������Լ������������ϵ���ó��𰸣�
��2������ƽ���ı��ε��ж��ó��ı���AFBDΪƽ���ı��Σ������ó�AF=![]() BC=BF������𰸣�
BC=BF������𰸣�
��3���������⻭��ͼ�Σ���CF=k�����ù��ɶ���������ɣ�
�⣺��1��S��ABC=S�ı���AFBD��
���ɣ�������ɵã�AD��EC��
��S��ADF=S��ABD��
��S��ACF=S��ADF=S��ABD��
��S��ABC=S�ı���AFBD��
��2����ABCΪ����ֱ�������Σ�����AB=AC����BAC=90�㣬
�������£�
��FΪBC���е㣬
��CF=BF��
��CF=AD��
��AD=BF��
�֡�AD��BF��
���ı���AFBDΪƽ���ı��Σ�
��AB=AC��FΪBC���е㣬
��AF��BC��
��ƽ���ı���AFBDΪ����
�ߡ�BAC=90�㣬FΪBC���е㣬
��AF=![]() BC=BF��
BC=BF��
���ı���AFBDΪ�����Σ�
��3����ͼ3��ʾ��

�ɣ�2��֪����ABCΪ����ֱ�������Σ�AF��BC��
��CF=k����GF=EF=CB=2k��
�ɹ��ɶ����ã�CG=![]() k��
k��
��CG=![]() CF��
CF��

 �ܿ�����ĩ��̾�ϵ�д�
�ܿ�����ĩ��̾�ϵ�д�