题目内容
函数y=x+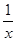 的图象如图所示,对该函数的性质的论断:
的图象如图所示,对该函数的性质的论断:
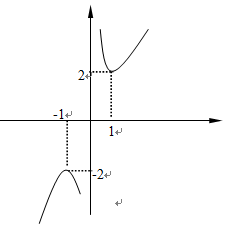
①该函数的图象是中心对称图形;②当x>0时,该函数在x=1时取得最小值;③当x>1时,y随x的增大而减小;④y的值不可能为-1,其中一定正确的有 ▲ .(填写编号)
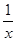 的图象如图所示,对该函数的性质的论断:
的图象如图所示,对该函数的性质的论断: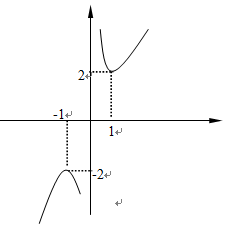
①该函数的图象是中心对称图形;②当x>0时,该函数在x=1时取得最小值;③当x>1时,y随x的增大而减小;④y的值不可能为-1,其中一定正确的有 ▲ .(填写编号)
①②④
根据关于原点对称的两点(a,a+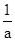 )、(-a,-a-
)、(-a,-a-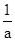 )都在函数y=x+
)都在函数y=x+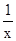 的图象上,由此可对①进行判断;当x>0,利用不等式x+
的图象上,由此可对①进行判断;当x>0,利用不等式x+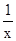 ≥2?x?
≥2?x?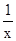 =2,而点(1,2)在函数图象上,于是可对②进行判断;观察图象得到当x>1时,y随x的增大而增大,由此可对③进行判断;利用中心对称的性质得到x<0时,最大值为-2,由此得到y的最大值为-2,于是可对④进行判断.
=2,而点(1,2)在函数图象上,于是可对②进行判断;观察图象得到当x>1时,y随x的增大而增大,由此可对③进行判断;利用中心对称的性质得到x<0时,最大值为-2,由此得到y的最大值为-2,于是可对④进行判断.
解答:解:当x=a,y=a+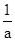 ,即点(a,a+
,即点(a,a+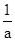 )函数y=x+
)函数y=x+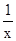 的图象上;当x=-a,y=-a-
的图象上;当x=-a,y=-a-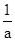 ,即点(-a,-a-
,即点(-a,-a-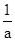 )函数y=x+
)函数y=x+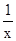 的图象上,而点(a,a+
的图象上,而点(a,a+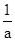 )与点(-a,-a-
)与点(-a,-a-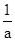 )关于原点中心对称,则该函数的图象是中心对称图形,所以①正确;
)关于原点中心对称,则该函数的图象是中心对称图形,所以①正确;
当x>0,x+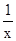 ≥2?x?
≥2?x?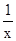 =2,即x>0时,该函数的有最小值为1,由图象得x=1时,y=2,所以②正确;
=2,即x>0时,该函数的有最小值为1,由图象得x=1时,y=2,所以②正确;
当x>1时,y随x的增大而增大,所以③错误;
由于该函数的图象是关于原点中心对称,则x<0时,最大值为-2,所以④正确.
故答案为①②④.
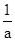 )、(-a,-a-
)、(-a,-a-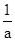 )都在函数y=x+
)都在函数y=x+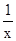 的图象上,由此可对①进行判断;当x>0,利用不等式x+
的图象上,由此可对①进行判断;当x>0,利用不等式x+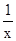 ≥2?x?
≥2?x?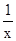 =2,而点(1,2)在函数图象上,于是可对②进行判断;观察图象得到当x>1时,y随x的增大而增大,由此可对③进行判断;利用中心对称的性质得到x<0时,最大值为-2,由此得到y的最大值为-2,于是可对④进行判断.
=2,而点(1,2)在函数图象上,于是可对②进行判断;观察图象得到当x>1时,y随x的增大而增大,由此可对③进行判断;利用中心对称的性质得到x<0时,最大值为-2,由此得到y的最大值为-2,于是可对④进行判断.解答:解:当x=a,y=a+
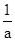 ,即点(a,a+
,即点(a,a+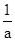 )函数y=x+
)函数y=x+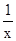 的图象上;当x=-a,y=-a-
的图象上;当x=-a,y=-a-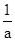 ,即点(-a,-a-
,即点(-a,-a-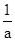 )函数y=x+
)函数y=x+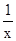 的图象上,而点(a,a+
的图象上,而点(a,a+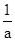 )与点(-a,-a-
)与点(-a,-a-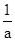 )关于原点中心对称,则该函数的图象是中心对称图形,所以①正确;
)关于原点中心对称,则该函数的图象是中心对称图形,所以①正确;当x>0,x+
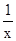 ≥2?x?
≥2?x?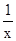 =2,即x>0时,该函数的有最小值为1,由图象得x=1时,y=2,所以②正确;
=2,即x>0时,该函数的有最小值为1,由图象得x=1时,y=2,所以②正确;当x>1时,y随x的增大而增大,所以③错误;
由于该函数的图象是关于原点中心对称,则x<0时,最大值为-2,所以④正确.
故答案为①②④.

练习册系列答案
相关题目
 图像得到直线y=
图像得到直线y= ,就是将直线y=
,就是将直线y=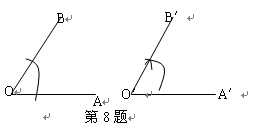
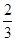 个单位
个单位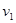 km/h,水流速度为
km/h,水流速度为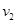 km/h (
km/h (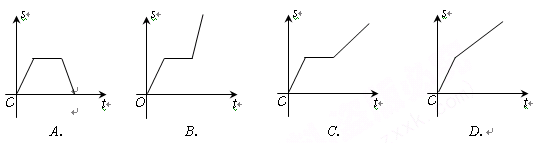
 中自变量
中自变量 的取值范围是___________.
的取值范围是___________. =
=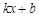 (k≠0)与坐标轴分别交于A、B两点,OA、OB的长分别
(k≠0)与坐标轴分别交于A、B两点,OA、OB的长分别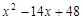 =0的两根(OA>OB).动点P从O点出发,沿路线O→B→A以每
=0的两根(OA>OB).动点P从O点出发,沿路线O→B→A以每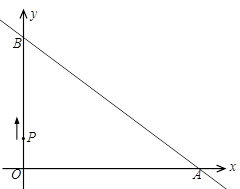
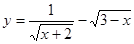 中自变量x的取值范围是
中自变量x的取值范围是 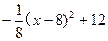 (1≤x≤16且x为整数)
(1≤x≤16且x为整数) 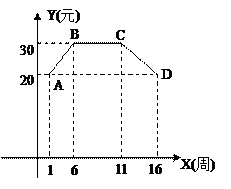
 图象上的是……………………………………( )
图象上的是……………………………………( ) )
)