题目内容
2. △ABD与△EBC都是等腰直角三角形,AD、CE为斜边,延长EA、DC交于点F.
△ABD与△EBC都是等腰直角三角形,AD、CE为斜边,延长EA、DC交于点F.(1)求证:∠AEB=∠DCB;
(2)求∠BEC的度数;
(3)求证:EF⊥DF.
分析 (1)欲证明∠AEB=∠DCB,只要证明△EAB≌△CBD即可.
(2)根据等腰直角三角形的性质即可解决问题.
(3)根据四边形内角和360°,只要证明∠CBE+∠F=180°即可解决问题.
解答 (1)证明:∵AB=BD,BE=BC,∠ABD=∠EBC,
∴∠EBA=∠CBD,
在△EBA和△CBD中,
$\left\{\begin{array}{l}{EB=CB}\\{∠EBA=∠CBD}\\{BA=BD}\end{array}\right.$,
∴△EAB≌△CBD,
∴∠AEB=∠BCD.
(2)解:∵CB=BA,∠EBC=90°,
∴∠BEC=∠BCE=45°.
(3)证明:∵∠AEB=∠BCD,∠BCD+∠BCF=180°,
∴∠AEB+∠BCF=180°,
∴∠CBE+∠F=180°,
∵∠CBE=90°,
∴∠F=90°,
∴EF⊥DF.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质、四边形内角和等知识,解题的关键是灵活运用所学知识解决问题,属于基础题,中考常考题型.

练习册系列答案
相关题目
10.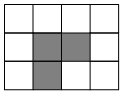 如图,在3×4的正方形网格中,黑色部分的图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是( )
如图,在3×4的正方形网格中,黑色部分的图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是( )
 如图,在3×4的正方形网格中,黑色部分的图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是( )
如图,在3×4的正方形网格中,黑色部分的图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是( )| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
 A、B两个城市的位置如图所示,那么B城在A城的北偏西30°方向.
A、B两个城市的位置如图所示,那么B城在A城的北偏西30°方向. 如图,直线l经过A(-3,0),B(0,6),过原点O的直线l1与直线l交于点P,使直线l、直线l1与坐标轴围成的三角形面积是△ABO的三分之一,则点P的坐标是(-4,-2)或(-2,2)或(-1,4).
如图,直线l经过A(-3,0),B(0,6),过原点O的直线l1与直线l交于点P,使直线l、直线l1与坐标轴围成的三角形面积是△ABO的三分之一,则点P的坐标是(-4,-2)或(-2,2)或(-1,4).