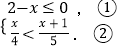题目内容
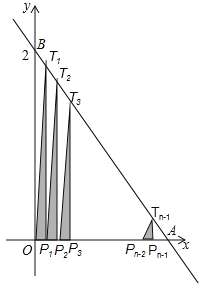
【题目】如图，直线
与两坐标轴分别交于A、B两点，将线段OA分成n等份，分点分别为P1，P2，P3，…，Pn﹣1，过每个分点作x轴的垂线分别交直线AB于点T1，T2，T3，…，Tn﹣1，用S1，S2，S3，…，Sn﹣1分别表示Rt△T1OP1，Rt△T2P1P2，…，Rt△Tn﹣1Pn﹣2Pn﹣1的面积，则当n=2015时，S1+S2+S3+…+Sn﹣1= ．
【答案】
．
【解析】
试题分析：∵P1，P2，P3，…，Pn﹣1是x轴上的点，且OP1=P1P2=P2P3=…=Pn﹣2Pn﹣1=
，
分别过点p1、p2、p3、…、pn﹣2、pn﹣1作x轴的垂线交直线
于点T1，T2，T3，…，Tn﹣1，
∴T1的横坐标为：，纵坐标为：
，∴S1=
=
，
同理可得：T2的横坐标为：
，纵坐标为：
，∴S2=
，
T3的横坐标为：
，纵坐标为：
，S3=
，
…
Sn﹣1=
），
∴S1+S2+S3+…+Sn﹣1=
=
=
，
∵n=2015，∴S1+S2+S3+…+S2014=
=．
故答案为：．
练习册系列答案
相关题目
【题目】市射击队为从甲、乙两名运动员中选拔一人参加省比赛，对他们进行了六次测试，测试成绩如表：
（1）把表中所空各项数据填写完整；
选手 | 选拔成绩/环 | 中位数 | 平均数 | |||||
甲 | 10 | 9 | 8 | 8 | 10 | 9 | ||
乙 | 10 | 10 | 8 | 10 | 7 | 9 | ||
（2）分别计算甲、乙六次测试成绩的方差；
（3）根据（1）、（2）计算的结果，你认为推荐谁参加省比赛更合适，请说明理由．
