题目内容
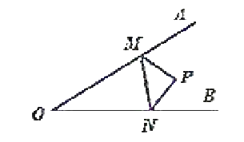
【题目】如图,![]() ,点
,点![]() 为
为![]() 内一点,
内一点,![]() ,点
,点![]() 分别在射线
分别在射线![]() 上,当
上,当![]() 的周长最小时,下列结论:①
的周长最小时,下列结论:①![]() ;②
;②![]() ;③
;③![]() 的周长最小值为24;④
的周长最小值为24;④![]() 的周长最小值为8;其中正确的序号为__________.
的周长最小值为8;其中正确的序号为__________.
【答案】①④
【解析】
分别作点P关于OA、OB的对称点P1、P2,连P1、P2,交OA于M,交OB于N,△PMN的周长=P1P2,然后证明△OP1P2是等边三角形,即可求解.
解:分别作点P关于OA、OB的对称点P1、P2,连P1、P2,交OA于M,交OB于N,
则OP1=OP=OP2,∠P1OA=∠POA,∠POB=∠P2OB,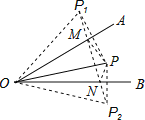
MP=P1M,PN=P2N,则△PMN的周长的最小值=P1P2
∴∠P1OP2=2∠AOB=60°,
∴△OP1P2是等边三角形,
∴∠MPN=∠OPM+∠OPN=∠OP1M+∠OP2N=120°
△PMN的周长=P1P2,
∴P1P2=OP1=OP2=OP=8,
∴①④正确,
故答案为①④

练习册系列答案
相关题目