题目内容
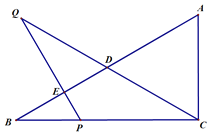
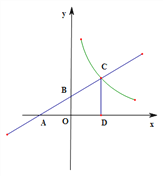
【题目】已知一次函数
的图象分别与坐标轴相交于A、B两点（如图所示），与反比例函数
的图象相交于点C，OA=3.
（1）求一次函数的解析式和点B的坐标；
（2）作CD⊥x轴，垂足为D，若
=1:3，求反比例函数
的解析式.
【答案】（1）一次函数的解析式为
，点B的坐标为（0，2）；（2）反比例函数的解析式为
【解析】分析：（1）由OA=3得A（-3，0），代入
得b=2，从而求出一次函数解析式，令x=0，则y=2，故点B的坐标为（0，2）；
（2）分别求出
和
，设出点C坐标，根据梯形面积求解即可.
详解：（1）∵OA=3
∴A（-3，0）
将A（-3，0）代入
中得b=2
∴一次函数的解析式为
令x=0得y=2
∴点B的坐标为（0，2）
(2)由题知
∵
=1:3
∴
=9
设C（m， 
），则有
解得m1=3，m2=-9(舍去)
∴C（3，4）
∵C（3，4）在反比例函数
上
∴反比例函数的解析式为
.
练习册系列答案
阅读快车系列答案
相关题目
【题目】观察表格：
|
|
| |
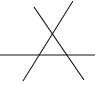
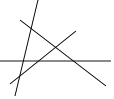
1条直线 0个交点 平面分成（1+1）块 | 2条直线 1个交点 平面分成（1+1+2）块 | 3条直线 （1+2）个交点 平面分成（1+1+2+3）块 | 4条直线 （1+2+3）个交点 平面分成（1+1+2+3+4）块 |
根据表格中的规律解答问题：
（1）5条直线两两相交，有 个交点，平面被分成 块；
（2）n条直线两两相交，有 个交点，平面被分成 块；
（3）应用发现的规律解决问题：一张圆饼切10刀（不许重叠），最多可得到 块饼．
