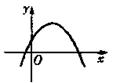题目内容
已知一抛物线与x轴的交点是A(-2,0)、B(1,0),且经过点C(2,8)
(1)求该抛物线的解析式;
(2)求该抛物线的顶点坐标;
(3)x取什么值时,函数值大于0? x取什么值时,函数值小于0?
(1)求该抛物线的解析式;
(2)求该抛物线的顶点坐标;
(3)x取什么值时,函数值大于0? x取什么值时,函数值小于0?
(1)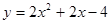 ;(2)
;(2)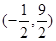 ;(3)
;(3)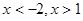 时,y>0;
时,y>0;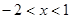 时,y<0
时,y<0
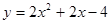 ;(2)
;(2)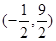 ;(3)
;(3)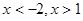 时,y>0;
时,y>0;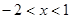 时,y<0
时,y<0试题分析:(1)根据A(-2,0)、B(1,0),可设两根式,再根据C(2,8)即可求得结果;
(2)将函数的解析式化为顶点式即可求得顶点坐标
(3)根据抛物线与x轴的交点以及抛物线的开口方向即可判断结果。
设
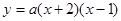
经过点C(2,8)
得a=2
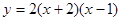
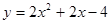
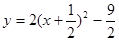
顶点坐标.
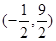
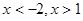 时,y>0
时,y>0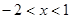 时,y<0
时,y<0点评:(1)第一问考查函数的基本性质及用待定系数法求函数的解析式,比较简单;
(2)第二问考查函数的对称轴和顶点坐标,解题的关键是将函数的解析式化为顶点式;
(3)第三问主要考查函数图象的特征。

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
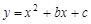 的图象经过点A(-1,0),B(1,-2),该图象与x轴的另一个交点为C,则AC长为__________ .
的图象经过点A(-1,0),B(1,-2),该图象与x轴的另一个交点为C,则AC长为__________ . 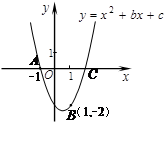
 时,
时, 有最大值为5,且它的图象经过点(2,3),求:
有最大值为5,且它的图象经过点(2,3),求: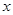 的取值范围.
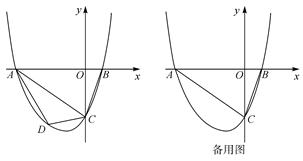
的取值范围. 的图象如图所示,则下列结论:
的图象如图所示,则下列结论:
 的两根之和大于1;②
的两根之和大于1;② ;
; 随
随 的增大而增大;④
的增大而增大;④ .
. 的图象与
的图象与 轴交点的坐标是
轴交点的坐标是 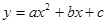 的图象如图所示,则函数
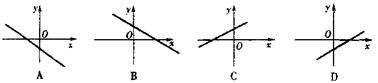
的图象如图所示,则函数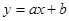 的图象是( )
的图象是( )