题目内容
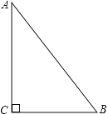
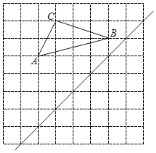
【题目】如图，在8×8的正方形网格中，每个小正方形的边长都是1，已知△ABC的三个顶点在格点上．
（1）画出△ABC关于直线l对称的△A1B1C1；
（2）在直线l上找一点P，使PA+PB的长最短；（不写作法，保留作图痕迹）
（3）△ABC 直角三角形（填“是”或“不是”），并说明理由．
【答案】（1）见解析；（2）见解析；（3）不是，理由见解析
【解析】
（1）利用网格特点和轴对称的性质画出A、B、C关于直线l的对称点A1、B1、C1即可；
（2）连接AB1交直线l于P，则利用两点之间线段最短可判断P点满足条件；
（3）利用勾股定理的逆定理可判断△ABC不是直角三角形．
（1）如图，△A1B1C1为所作；
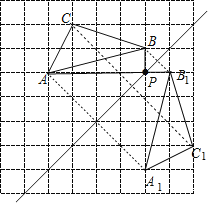
（2）如图，点P为所作；
（3））△ABC不是直角三角形．
理由如下：∵AC＝
＝
，BC＝
＝
，AB＝
＝
，
而（）2+（）2≠（）2，
∴AC2+BC2≠AB2，
∴△ABC不是直角三角形．
故答案为不是．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
