题目内容
【题目】(1)如图1,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数;
(2)如图2,AB∥CD,AB=CD,BF=DE,求证:∠AEF=∠CFB.

【答案】(1) 20°;(2)见解析
【解析】
(1)推出EF∥BC,根据平行线性质求出∠ACB,求出∠FCB,根据角平分线求出∠ECB,根据平行线的性质推出∠FEC=∠ECB,代入即可.
(2)根据平行线的性质、线段间的和差关系证得∠B=∠D、BE=DF;然后由全等三角形的判定定理SAS推知△ABE≌△CDF;最后由全等三角形的对应角相等证得结论;
(1)∵EF∥AD,AD∥BC,
∴EF∥BC,
∴∠ACB+∠DAC=180°,
∵∠DAC=120°,
∴∠ACB=60°,
又∵∠ACF=20°,
∴∠FCB=∠ACB-∠ACF=40°,
∵CE平分∠BCF,
∴∠BCE=20°,
∵EF∥BC,
∴∠FEC=∠ECB,
∴∠FEC=20°;
(2)∵AB∥CD(已知),
∴∠B=∠D,
又∵BF=DE,
∴BF-EF=DE-EF,即BE=DF,
∴在△ABE和△CDF中,
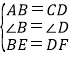 ,
,
∴△ABE≌△CDF(SAS),
∴∠A=∠C,
∴∠BEA=∠DFC,
∴:∠AEF=∠CFB.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目





