Question

【题目】某地震救援队探测出某建筑物废墟下方点C处有生命迹象，已知废墟一侧地面上两探测点A，B相距3米，探测线与地面的夹角分别是30°和60°（如图），试确定生命所在点C的深度．（结果保留根号）

Answer 1

【答案】解：如图，过点C作CD⊥AB交AB的延长线于D点．

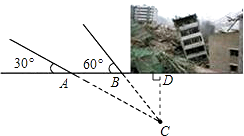
∵探测线与地面的夹角为30°和60°，

∴∠CAD=30°∠CBD=60°，

根据三角形的外角定理，得∠BCA=∠CBD﹣∠CAD=30°，

即∠BCA=∠CAD=30°，

∴BC=AB=3米，

在Rt△BDC中，CD=BCsin60°=3× = 米．

答：生命所在点C的深度约为 米．

【解析】过点C作CD⊥AB交AB的延长线于D点，依据题意可得到∠CAD=30°，∠CBD=60°，接下来，依据三角形的外角的性质可求得∠BCA=30°，则BC=AB=3米，最后，在Rt△BDC中利用特殊锐角三角函数值求解即可.