题目内容
【题目】成都一机械厂接到生产一批机器设备的订单,要求必须在12天(含12天)内完成.已知每台机械设备的成本价为800元,该厂平时每天能生产该设备20台。为了加快进度,该厂采取工人分批日夜加班的方式,每天的生产量得到了提高。这样,第一天生产了22台,以后每天生产的设备都比前一天多2台。但由于机器损耗等原因,当每天生产的设备达到30台后,每多生产1台机械设备,当天生产的所有生产的设备每台的成本就增加20元。设生产这批设备的时间为x天,每天生产的机械设备为y台。
(1)直接写出y与x之间的函数关系式,并写出自变量x的取值范围。
(2)若这批机器设备的订购价格为每台1200元,该机械厂决定把获得最高利润的那一天的全部利润用来补贴困难职工。设该厂每天的利润为W元,试求出W与x之间的函数关系式,并求出该机械厂用来补贴给困难职工多少钱?
【答案】(1)y=2x+20(1≤x≤12);(2)12000元.
【解析】
试题解析:(1)根据该车间平时每天能生产设备20台,第一天生产了22台,以后每天生产的设备都比前一天多2台,直接得出生产这批设备的时间为x天,与每天生产的设备为y台之间的函数关系式;
(2)根据基本等量关系是:利润=(每台设备购价-每台设备成本价-增加的其他费用)×生产量即可得出答案.
试题解析:(1)∵该车间平时每天能生产设备20台,第一天生产了22台,以后每天生产的设备都比前一天多2台,
∴由题意可得出,生产这批设备的时间为x天,每天生产的设备为y台之间的函数关系式为:y=2x+20(1≤x≤12);
(2)当1≤x≤5时,W=(1200-800)×(2x+20)=800x+8000,
此时W随着x的增大而增大,
∴当x=5时,W最大值=12000;
当5<x≤12时,
W=[1200-800-20×(2x+20-30)]×(2x+20)
=-80(x-2.5)2+12500,
此时函数图象开口向下,在对称右侧,W随着x的增大而减小,又天数x为整数,
∴当x=6时,W最大值=11520元.
∵12000>11520,
∴当x=5时,W最大,且W最大值=12000元.
综上所述:
W=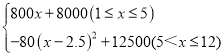 .
.
∴该车间捐献给困难职工12000元.