题目内容
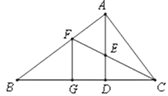
【题目】如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,∠ACB的平分线交AD于点E,交AB于点F,FG⊥BC于点G.求证:AE=FG.
【答案】证明见解析
【解析】
根据角平分线上的点到两边的距离相等可得:FG=FA;则只要在确定FA与AE的关系即可确定AE与FG之间的关系;在直角三角形AFC中∠AFC+∠ACF=90°,在直角三角形CDE中,∠DEC+∠ECD=90°,根据角平分线的性质可知:∠ACF=∠DCE,则∠AFC=∠DEC,又知∠AEF=∠DEC,则∠AFC=∠AEF,所以AE=FA,则AE=FG.
解:∵CF平分∠ACB,FA⊥AC,FG⊥BC
∴FG=FA
∵∠AFC+∠ACF=90°,∠DEC+∠ECD=90°,且∠ACF=∠ECD
∴∠AFC=∠DEC
∵∠AEF=∠DEC
∴∠AFC=∠AEF
∴AE=FA
∴AE=FG.

练习册系列答案
相关题目





