题目内容
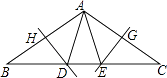
【题目】如图,点A是双曲线y=![]() 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .
在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .

【答案】y=﹣![]() .
.
【解析】
试题分析:连结OC,作CD⊥x轴于D,AE⊥x轴于E,设A点坐标为(a,![]() ),利用反比例函数的性质得到点A与点B关于原点对称,则OA=OB,再根据等腰直角三角形的性质得OC=OA,OC⊥OA,然后利用等角的余角相等可得到∠DCO=∠AOE,则根据“AAS”可判断△COD≌△OAE,所以OD=AE=
),利用反比例函数的性质得到点A与点B关于原点对称,则OA=OB,再根据等腰直角三角形的性质得OC=OA,OC⊥OA,然后利用等角的余角相等可得到∠DCO=∠AOE,则根据“AAS”可判断△COD≌△OAE,所以OD=AE=![]() ,CD=OE=a,于是C点坐标为(﹣
,CD=OE=a,于是C点坐标为(﹣![]() ,a),最后根据反比例函数图象上点的坐标特征确定C点所在的函数图象解析式.
,a),最后根据反比例函数图象上点的坐标特征确定C点所在的函数图象解析式.
试题解析:连结OC,作CD⊥x轴于D,AE⊥x轴于E,如图,
设A点坐标为(a,![]() ),
),
∵A点、B点是正比例函数图象与双曲线y=![]() 的交点,
的交点,
∴点A与点B关于原点对称,
∴OA=OB
∵△ABC为等腰直角三角形,
∴OC=OA,OC⊥OA,
∴∠DOC+∠AOE=90°,
∵∠DOC+∠DCO=90°,
∴∠DCO=∠AOE,
∵在△COD和△OAE中
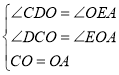
∴△COD≌△OAE(AAS),
∴OD=AE=![]() ,CD=OE=a,
,CD=OE=a,
∴C点坐标为(﹣![]() ,a),
,a),
∵﹣![]() a=﹣4,
a=﹣4,
∴点C在反比例函数y=﹣![]() 图象上.
图象上.

练习册系列答案
相关题目