题目内容
【题目】如图,四边形OBCD中的三个顶点在⊙O上,点A是优弧BD上的一个动点(不与点B、D重合).

(1)当圆心O在∠BAD内部,∠ABO+∠ADO=60°时,∠BOD= ;
(2)当圆心O在∠BAD内部,四边形OBCD为平行四边形时,求∠A的度数;
(3)当圆心O在∠BAD外部,四边形OBCD为平行四边形时,请直接写出∠ABO与∠ADO的数量关系.
【答案】(1)120 °;(2)60°;(3)60°.
【解析】试题分析:(1)连接OA,如图1,根据等腰三角形的性质得∠OAB=∠ABO,∠OAD=∠ADO,则∠OAB+∠OAD=∠ABO+∠ADO=60°,然后根据圆周角定理易得∠BOD=2∠BAD=120°;(2)根据平行四边形的性质得∠BOD=∠BCD,再根据圆周角定理得∠BOD=2∠A,则∠BCD=2∠A,然后根据圆内接四边形的性质由∠BCD+∠A=180°,易计算出∠A的度数;(3)讨论:当∠OAB比∠ODA小时,如图2,与(1)一样∠OAB=∠ABO,∠OAD=∠ADO,则∠OAD﹣∠OAB=∠ADO﹣∠ABO=∠BAD,由(2)得∠BAD=60°,
所以∠ADO﹣∠ABO=60°;当∠OAB比∠ODA大时,用样方法得到∠ABO﹣∠ADO=60°.
试题解析:(1)连接OA,如图1,
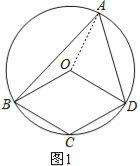
∵OA=OB,OA=OD, ∵∠OAB=∠ABO,∠OAD=∠ADO, ∴∠OAB+∠OAD=∠ABO+∠ADO=60°,即∠BAD=60°,
∴∠BOD=2∠BAD=120°;
(2)∵四边形OBCD为平行四边形, ∴∠BOD=∠BCD, ∵∠BOD=2∠A, ∴∠BCD=2∠A,
∵∠BCD+∠A=180°,即3∠A=180°, ∴∠A=60°;
(3)当∠OAB比∠ODA小时,如图2,

∵OA=OB,OA=OD, ∵∠OAB=∠ABO,∠OAD=∠ADO, ∴∠OAD﹣∠OAB=∠ADO﹣∠ABO=∠BAD,
由(2)得∠BAD=60°, ∴∠ADO﹣∠ABO=60°; 当∠OAB比∠ODA大时,
同理可得∠ABO﹣∠ADO=60°, 综上所述,|∠ABO﹣∠ADO|=60°.

 53随堂测系列答案
53随堂测系列答案