题目内容
【题目】如图,菱形ABCD中,AE⊥BC于点E,BE=CE,AD=4cm.
(1)求菱形ABCD的各角的度数;
(2)求AE的长.

【答案】(1)证明见解析(2)2![]() cm
cm
【解析】试题分析:(1)连结AC,根据垂直平分线的性质及菱形的性质可得△ABC为等边三角形,即可得到结果;
(2)根据菱形的性质,再结合勾股定理即可求得结果。
(1)如图,连结AC,
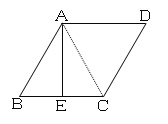
∵AE⊥BC于点E,BE=CE,即AE垂直且平分线段BC,
∴AC=AB(线段垂直平分线上的点到线段两端点的距离相等),
又∵BC=AB(菱形的四边相等),
∴△ABC为等边三角形,
∴∠B=60°,
∵AD∥BC,
∴∠BAD=180-60°=120°(两直线平行,同旁内角互补),
∴∠D=∠B=60°,∠BCD=∠BAD=120°(菱形的对角相等),
即菱形ABCD的各角的度数分别为: 60°、120°、60°、120°;
(2)∵菱形的四边相等,
∴BC=AB=AD=4cm,
又∵BE=CE,
∴BE=2cm,
在Rt△ABE中,由勾股定理得AE=![]() =
=![]() =
=![]() =2
=2![]() cm.
cm.

练习册系列答案
相关题目



