题目内容
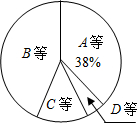
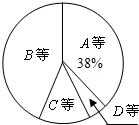
某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和如图扇形统计图.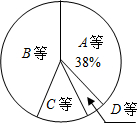
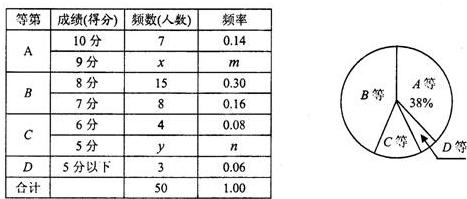
| 等次 | 成绩(得分) | 频数(人数) | 频率 |
| A | 10分 | 7 | 0.14 |
| 9分 | x | m | |
| B | 8分 | 15 | 0.30 |
| 7分 | 8 | 0.16 | |
| C | 6分 | 4 | 0.08 |
| 5分 | y | n | |
| D | 5分以下 | 3 | 0.06 |
| 合计 | 50 | 1.00 |
(2)分别求出中位数所在等次,及平均数,众数.
(3)如果该校九年级共有男生400名,试估计这400名男生中成绩达到A等和B等的人数共有多少人?
解:(1)x=50×38%-7=12,
y=50-49=1,
m=12÷50=0.24,
n=1÷50=0.02;
(2)∵共50人,中位数是第25和第26人的平均数,
∴中位数所在等次是B级;
平均数是 =7.81分,
=7.81分,
8分出现的次数最多,故众数是8分.
(3)达到A等和B等的人数为:(0.14+0.24+0.3+0.16)×200=168人.
分析:(1)首先根据扇形统计图计算A等的人数,从而计算出x的值,再根据总数计算y的值,最后根据频率=频数÷总数,计算m,n的值;
(2)根据总人数和每个小组的频数确定中位数、利用加权平均数的计算方法求平均数,根据众数的定义求众数即可;
(3)首先计算样本中达到A等和B等的人数的频率,进一步估计总体中的人数;
点评:本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
y=50-49=1,
m=12÷50=0.24,
n=1÷50=0.02;
(2)∵共50人,中位数是第25和第26人的平均数,
∴中位数所在等次是B级;
平均数是
 =7.81分,
=7.81分,8分出现的次数最多,故众数是8分.
(3)达到A等和B等的人数为:(0.14+0.24+0.3+0.16)×200=168人.
分析:(1)首先根据扇形统计图计算A等的人数,从而计算出x的值,再根据总数计算y的值,最后根据频率=频数÷总数,计算m,n的值;
(2)根据总人数和每个小组的频数确定中位数、利用加权平均数的计算方法求平均数,根据众数的定义求众数即可;
(3)首先计算样本中达到A等和B等的人数的频率,进一步估计总体中的人数;
点评:本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A、B、C、D四等,并绘制成下面的频数分布表和扇形统计图.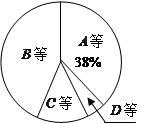
| 等第 | 成绩(得分) | 频数(人数) | 频率 |
| A | 10分 | 7 | 0.14 |
| 9分 | x | m | |
| B | 8分 | 15 | 0.30 |
| 7分 | 8 | 0.16 | |
| C | 6分 | 4 | 0.08 |
| 5分 | y | n | |
| D | 5分以下 | 3 | 0.06 |
| 合计 | | 50 | 1.00 |
(2)求表示得分为C等的扇形的圆心角的度数;
(3)如果该校九年级共有男生200名,试估计这200名男生中成绩达到A等和B等的人数共有多少人?
 14、某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.
14、某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.