题目内容
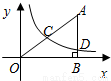
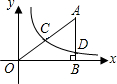在直角坐标系中，有如图所示的Rt△ABO，AB⊥x轴于点B，斜边AO=10，sin∠AOB=| 4 |
| 5 |
| k |
| x |
（6，2）
（6，2）
．分析：由斜边AO=10，sin∠AOB=
，根据三角函数的定义可得到AB=8，再由勾股定理得到AB=6，即得到A点坐标为（6，8），从而得到AO的中点C的坐标，代入反比例函数解析式确定k，然后令x=6，即可得到D点的纵坐标．
| 4 |
| 5 |
解答：解：∵斜边AO=10，sin∠AOB=
，
∴sin∠AOB=
=
=
，
∴AB=8，
∴OB=
=6，
∴A点坐标为（6，8），
而C点为OA的中点，
∴C点坐标为（3，4），
又∵反比例函数y=
（k＞0）的图象经过点C，
∴k=4×3=12，即反比例函数的解析式为y=
，
∵D点在反比例函数的图象上，且它的横坐标为6，
∴当x=6，y=
=2，
所以D点坐标为（6，2）．
故答案为：（6，2）．
| 4 |
| 5 |
∴sin∠AOB=
| AB |
| AO |
| AB |
| 10 |
| 4 |
| 5 |
∴AB=8，
∴OB=
| 102-82 |
∴A点坐标为（6，8），
而C点为OA的中点，
∴C点坐标为（3，4），
又∵反比例函数y=
| k |
| x |
∴k=4×3=12，即反比例函数的解析式为y=
| 12 |
| x |
∵D点在反比例函数的图象上，且它的横坐标为6，
∴当x=6，y=
| 12 |
| 6 |
所以D点坐标为（6，2）．
故答案为：（6，2）．
点评：本题考查了用待定系数法确定反比例的解析式以及正弦的定义和勾股定理以及求线段中点坐标．根据锐角三角函数得出AB的长是解题关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
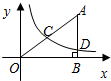在直角坐标系中，有如图所示的Rt△ABO，AB⊥x轴于点B，斜边AO=10，sin∠AOB=
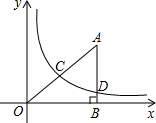在直角坐标系中，有如图所示的Rt△ABO，AB⊥x轴于点B，OB=5，AD=3．反比例函数
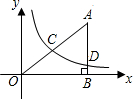在直角坐标系中，有如图所示的Rt△ABO，AB⊥x轴于点B，斜边AO=10，sin∠AOB=
，反比例函数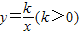
的图象经过AO的中点C，且与AB交于点D，则点D的坐标为 ．