题目内容
已知抛物线y=-x2-2kx+3k2(k>0)交x轴于A、B两点,交y轴于点C,以AB为直径的⊙E交y轴于点D、F(如下图),且DF=4,G是劣弧![]() 上的动点(不与点A、D重合),直线CG交x轴于点P.
上的动点(不与点A、D重合),直线CG交x轴于点P.

求抛物线的解析式;
当直线CG是⊙E的切线时,求tan∠PCO的值.
当直线CG是⊙E的割线时,作GM⊥AB,垂足为H,交PF于点M,交⊙E于另一点N,设MN=t,GM=u,求u关于t的函数关系式.
答案:
解析:
解析:
|
(1)解方程-x2-2kx+3k2=0. 得x1=-3k,x2=k 由题意知OA=|-3k|=3k,OB=|k|=k. ∵直径AB⊥DF.∴OD=OF= ∵ ∴3k·k=2×2,得k=± 则所求的抛物线的解析式为 (2)由(1)可知AO= 连结EG, ∵CG切⊙E于G,∴∠PGE=∠POC=90°, ∴Rt△PGE∽Rt△POC.∴ 由切割线定理得 PO=PA+AO=PA+ 代入(﹡)式整理得PA2+ 解得PA=3- ∴tan∠PCO= ∴GN∥CF,∴△PGH∽△PCO, ∴ 同理 ∵CO=4,OF=2,∴HM= ∴GM=3MN,即u=3t(0<t≤ |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

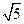 ,试求m的值;
,试求m的值; 直角坐标系中,用列表描点法作出抛物线的图象,并根据图象写出x取何值时,函
直角坐标系中,用列表描点法作出抛物线的图象,并根据图象写出x取何值时,函