Question

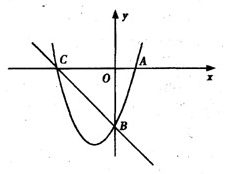
如图，已知抛物线y＝－x²＋bx＋c与x轴负半轴交于点A，与y轴正半轴交于点B，且OA＝OB．

1.求b＋c的值

2.若点C在抛物线上，且四边形OABC是平行四边形，试求抛物线的解析式；

3.在（2）的条件下，作∠OBC的角平分线，与抛物线交于点P，求点P的坐标．

 

Answer 1

 

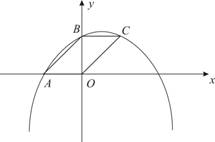
1.因为抛物线y＝－x²＋bx＋c与y轴正半轴交于点B，所以点B的坐标为（0，c）．…… 1分

因为OA＝OB，所以点A的坐标为（－c，0）．…… 2分

将点A（－c，0）代入y＝－x²＋bx＋c，得－c²＋bc＋c＝0．

因为c≠0，整理，得b＋c＝1．…… 4分

2.如果四边形OABC是平行四边形，那么BC//AO，BC＝AO．

因此点C的坐标可以表示为（c，c）．…… 5分

当点C（c，c）落在抛物线y＝－x²＋bx＋c上时，得－c²＋bc＋c＝c．

整理，得b＝c．…… 6分

结合第（1）题的结论b＋c＝1，得．…… 7分

此时抛物线的解析式为．…… 8分

3.过点P作PM⊥y轴，垂足为M．

因为BP平分∠CBO，所以△BPM是等腰直角三角形．9分

设点P的坐标为，

由BM＝PM，列方程．…… 10分

解得或（舍去）．…… 11分

所以，点P的坐标为．…… 12分

解析:（1）因为抛物线y＝－x²＋bx＋c与y轴正半轴交于点B，所以点B的坐标为（0，c）．点A的坐标为（－c，0）．代入y＝－x²＋bx＋c，求得b＋c的值

（2）根据四边形OABC是平行四边形，得出点C的坐标可以表示为（c，c）进行解答

（3）过点P作PM⊥y轴，垂足为M．证得△BPM是等腰直角三角形