Question

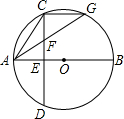如图，已知AB是⊙O的直径，弦CD⊥AB于E，F是CE上的一点，且FC=FA，延长AF交⊙O于G，连接CG．
（1）试判断△ACG的形状（按边分类），并证明你的结论；
（2）若⊙O的半径为5，OE=2，求CF•CD之值．

Answer 1

分析：（1）△ACG是等腰三角形，只要证明∠G=∠CAG，可以转化为证明

AD

=

AC

即可．
（2）连接AD，BC，易证△ACF∽△DCA，得到AC：CD=CF：AC，即AC²=CF•CD．再根据垂径定理得到AC²=AE²+CE²就可以求出．

解答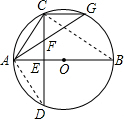：解：（1）△ACG是等腰三角形．
证明如下：
∵CD⊥AB，∴

AD

=

AC

．（1分）
∴∠G=∠ACD，（2分）
∵FC=FA，
∴∠ACD=∠CAG，（3分）
∴∠G=∠CAG，
∴△ACG是等腰三角形．（4分）

（2）连接AD，BC，（5分）
由（1）知

AC

=

AD

，
∴AC=AD．
∴∠D=∠ACD，（6分）
∴∠D=∠G=∠CAG，
又∵∠ACF=∠DCA，
∴△ACF∽△DCA，（7分）
∴AC：CD=CF：AC，
即AC²=CF•CD，（8分）
∵CD⊥AB，（9分）
∴AC²=AE²+CE²=（5-2）²+（5²-2²）=30．（11分）
∴CF•CD=30．（12分）

点评：证明等腰三角形可以依据等角对等角证明；第二问中利用了相似三角形的性质和垂径定理的推论．