题目内容
【题目】如图,直线 ![]() 与x轴交于点A,与直线 y=kx-3交于点C(c,6),直线
与x轴交于点A,与直线 y=kx-3交于点C(c,6),直线 ![]() 与y轴交于点B,连接AB.
与y轴交于点B,连接AB.
(1)求k的值;
(2)求证:∠CAO=∠BAO;
(3)P为OA上一点,连结PB,M为PB中点,延长MO交直线AC于点N,若OP=x, ![]() ,求y关于x的函数表达式.
,求y关于x的函数表达式.
【答案】
(1)解:∵C(c,6)y=![]() x+3,
x+3,
∴![]() c+3=6,
c+3=6,
∴c=4,
∴C(4,6),
又 ∵ C(4,6)在y=kx-3 上,
∴4k-3=6,
∴k=![]() .
.
(2)证明:∵AC所在直线方程为:y=![]() x+3,
x+3,
∴D(0,3),A(-4,0),
∴AO=4,DO=3,
∴AD=5,
又∵BC所在的直线方程为:y=![]() x-3,
x-3,
∴B(0,-3),
∴BO=3,
∴AB=5,
在△ADO和△ABO中,
∵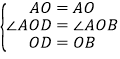 ,
,
∴△ADO≌△ABO,
∴∠CAO=∠BAO.
(3)解:过M作ME⊥OP,作NF⊥y轴,设N(a,![]() a+3),
a+3),
∴Rt△OEM∽Rt△NFO,
∴![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴a=![]() ,
,
又∵![]() =y,
=y,
∴![]() =y,
=y,
∴y=![]() .
.
∴y关于x的函数表达式为:y=![]() .
.
【解析】
(1)由待定系数法得出c=4,又 ∵由C(4,6)在y=kx-3 上,得出k的值.
(2)由AC和BC所在直线方程方可得出D(0,3),A(-4,0),B(0,-3);从而可以利用全等三角形的判定SAS得出△ADO≌△ABO,再根据全等三角形的性质得出∠CAO=∠BAO.
(3)过M作ME⊥OP,作NF⊥y轴,设N(a,![]() a+3),根据已知条件可以证明Rt△OEM∽Rt△NFO,再根据相似三角形的性质可以得出
a+3),根据已知条件可以证明Rt△OEM∽Rt△NFO,再根据相似三角形的性质可以得出 ![]() =
=![]() =
=![]() ,从而得出a=
,从而得出a=![]() ,又由
,又由![]() =y,得出y=
=y,得出y=![]() .
.
【考点精析】本题主要考查了确定一次函数的表达式和相似三角形的判定与性质的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.

【题目】2020年1月以来,由于新型冠状病毒(COVID-19)的肆虐,口罩市场出现热卖,某旗舰网店用8000元购进甲、乙两种口罩,销售完后共获利2800元,进价和售价如右表:
品名 | 甲种口罩 | 乙种口罩 |
进价(元/袋) | 20 | 25 |
售价(元/袋) | 26 | 35 |
(1)求该网店购进甲、乙两种口罩各多少袋?
(2)该网店第二次以原价购进甲、乙、两种口罩,购进乙种口罩袋数不变,而购进甲种口罩袋数是第一次的2倍.甲种口罩按原售价出售,而乙种口罩让利销售.若两种口罩销售完毕,要使第二次销售活动获利不少于3680元,乙种口罩最低售价为每袋多少元?






