题目内容
已知⊙O1与⊙O2的半径分别是方程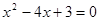 的两实根,且
的两实根,且 ,若这两个圆相切,则t =
,若这两个圆相切,则t =
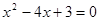 的两实根,且
的两实根,且 ,若这两个圆相切,则t =
,若这两个圆相切,则t = 2或0.
试题分析:先解方程求出⊙O1、⊙O2的半径,再分两圆外切和两圆内切两种情况列出关于t的方程讨论求解.
试题解析:∵⊙O1、⊙O2的半径分别是方程x2-4x+3=0的两根,
解得⊙O1、⊙O2的半径分别是1和3.
①当两圆外切时,圆心距O1O2=t+2=1+3=4,解得t=2;
②当两圆内切时,圆心距O1O2=t+2=3-1=2,解得t=0.
∴t为2或0.
考点: 1.圆与圆的位置关系;2.解一元二次方程-因式分解法.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 ,求
,求 的值。
的值。 (2)
(2)
 =0
=0