题目内容
【题目】“五·一”期间，九年一班同学从学校出发，去距学校6千米的本溪水洞游玩，同学们分为步行和骑自行车两组，在去水洞的全过程中，骑自行车的同学比步行的同学少用40分钟，已知骑自行车的速度是步行速度的3倍．
（1）求步行同学每分钟走多少千米？
（2）如图是两组同学前往水洞时的路程y（千米）与时间x（分钟）的函数图象．
完成下列填空：
①表示骑车同学的函数图象是线段__________；
②已知A点坐标（30，0），则B点的坐标为（________）．
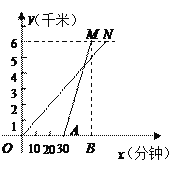
【答案】AM（50，0）
【解析】
（1）关键描述语：“骑自行车的同学比步行的同学少用40分钟”；等量关系为：步行的同学所用的时间＝骑自行车的同学所用的时间＋40；
（2）①函数图象的斜率为骑自行车和步行时的速率，骑自行车的速率快，故斜率大，故AM线段为骑车同学的函数图象；
②根据题中所的条件，可将线段AM的函数关系式表示出来，从而可将可将B点的坐标求出．
（1）设步行同学每分钟走
千米，则骑自行车同学每分钟走
千米，
根据题意，得：
，
，
经检验，是原方程的解，
答：步行同学每分钟走
千米；
（2）①骑车同学的速度快，即斜率大，故为线段AM；
②由（1）知，线段AM的斜率为：3x＝
，
设一次函数关系式为：y＝x＋b
将点A的坐标（30，0）代入可得：b＝9，
∴y＝x9．
当y＝6时，x＝50．
故点B的坐标为（50，0）．
练习册系列答案
相关题目
