题目内容
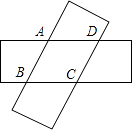
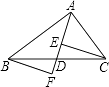
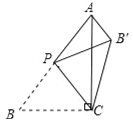
【题目】如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是AB边上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,得到△B′CP,连接B′A,则下列判断:
①当AP=BP时,AB′∥CP;
②当AP=BP时,∠B′PC=2∠B′AC
③当CP⊥AB时,AP=![]() ;
;
④B′A长度的最小值是1.
其中正确的判断是 (填入正确结论的序号)
【答案】①②④.
【解析】
试题分析:①∵在△ABC中,∠ACB=90°,AP=BP,∴AP=BP=CP,∴∠B=∠BPC=![]() (180°﹣∠APB′),由折叠的性质可得:CP=B′P,∠CPB′=∠BPC=
(180°﹣∠APB′),由折叠的性质可得:CP=B′P,∠CPB′=∠BPC=![]() (180°﹣∠APB′),∴AP=B′P,∴∠AB′P=′B′AP=
(180°﹣∠APB′),∴AP=B′P,∴∠AB′P=′B′AP=![]() (180°﹣∠APB′),∴∠AB′P=∠CPB′,∴AB′∥CP;故①正确;
(180°﹣∠APB′),∴∠AB′P=∠CPB′,∴AB′∥CP;故①正确;
②∵AP=BP,∴PA=PB′=PC=PB,∴点A,B′,C,B在以P为圆心,PA长为半径的圆上,∵由折叠的性质可得:BC=B′C,∴![]() ,∴∠B′PC=2∠B′AC;故②正确;
,∴∠B′PC=2∠B′AC;故②正确;
③当CP⊥AB时,∠APC=∠ACB,∵∠PAC=∠CAB,∴△ACP∽△ABC,∴![]() ,∵在Rt△ABC中,由勾股定理可知:AC=
,∵在Rt△ABC中,由勾股定理可知:AC=![]() =
=![]() =4,∴AP=
=4,∴AP=![]() =
=![]() ;故③错误;
;故③错误;
④由轴对称的性质可知:BC=CB′=3,∵CB′长度固定不变,∴当AB′+CB′有最小值时,AB′的长度有最小值.
根据两点之间线段最短可知:A.B′、C三点在一条直线上时,AB′有最小值,∴AB′=AC﹣B′C=4﹣3=1.故④正确.
故答案为:①②④.

练习册系列答案
相关题目