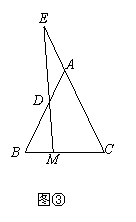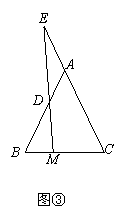题目内容
已知，在等腰△ABC中，AB=AC，分别延长BA，CA到D，E点，使DA=AB，EA=CA，则四边形BCDE是
- A.任意四边形
- B.矩形
- C.菱形
- D.正方形
B
分析：由一组对边平行且相等可得其为平行四边形，再由一角为90°且邻边不等可得其为矩形．
解答：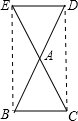
解：如图所示，
∵AC=AE，AB=AD
∴四边形BCDE为平行四边形，
∵AB=AE，∴∠AEB=∠ABE，
∵∠BAC+∠ABC+∠ACB=180°
∠ABC=∠ACB
∴∠ABC+∠EBA=90°
∴四边形BCDE为矩形．
故选B．
点评：熟练掌握矩形的判定，会证明一个四边形是矩形所满足的条件．
分析：由一组对边平行且相等可得其为平行四边形，再由一角为90°且邻边不等可得其为矩形．
解答：
解：如图所示，∵AC=AE，AB=AD
∴四边形BCDE为平行四边形，
∵AB=AE，∴∠AEB=∠ABE，
∵∠BAC+∠ABC+∠ACB=180°
∠ABC=∠ACB
∴∠ABC+∠EBA=90°
∴四边形BCDE为矩形．
故选B．
点评：熟练掌握矩形的判定，会证明一个四边形是矩形所满足的条件．
练习册系列答案
全能练考卷系列答案
一课一练课时达标系列答案
相关题目
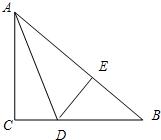22、已知：在等腰Rt△ABC中，AC=BC∠C=90°，AD平分∠BAC，DE⊥AB于点E，AB=15cm，
