题目内容
 22、已知:在等腰Rt△ABC中,AC=BC∠C=90°,AD平分∠BAC,DE⊥AB于点E,AB=15cm,
22、已知:在等腰Rt△ABC中,AC=BC∠C=90°,AD平分∠BAC,DE⊥AB于点E,AB=15cm,(1)求证:BD+DE=AC.
(2)求△DBE的周长.
分析:(1)因为AC=BC=BD+CD,只要证明CD=DE即可,又因为AD平分∠BAC,则CD=DE;
(2)由(1)可知AC=BD+DE,由CD=DE,AD=AD,∠C=∠AED=90°,可证△ACD≌△AED,则AC=AE,所以BD+DE+BE=AC+BE=AE+BE=AB.
(2)由(1)可知AC=BD+DE,由CD=DE,AD=AD,∠C=∠AED=90°,可证△ACD≌△AED,则AC=AE,所以BD+DE+BE=AC+BE=AE+BE=AB.
解答:解: (1)∵AD平分∠BAC,DE⊥AB,∠C=90°,
(1)∵AD平分∠BAC,DE⊥AB,∠C=90°,
∴CD=DE,
∴BC=BD+CD=BD+DE,
AC=BC,
∴AC=BD+DE;
(2)∵CD=DE,AD=AD,∠C=∠AED=90°,
∴△ACD≌△AED,
∴AC=AE,
∵AC=BD+DE,
∴BD+DE=AE,
∴△BDE周长=BD+DE+BE=AE+BE=AB=15cm.
 (1)∵AD平分∠BAC,DE⊥AB,∠C=90°,
(1)∵AD平分∠BAC,DE⊥AB,∠C=90°,∴CD=DE,
∴BC=BD+CD=BD+DE,
AC=BC,
∴AC=BD+DE;
(2)∵CD=DE,AD=AD,∠C=∠AED=90°,
∴△ACD≌△AED,
∴AC=AE,
∵AC=BD+DE,
∴BD+DE=AE,
∴△BDE周长=BD+DE+BE=AE+BE=AB=15cm.
点评:本题考查了角平分线性质,等腰三角形的性质;根据性质将线段长进行等效转化是一种常常用到的方法,注意掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

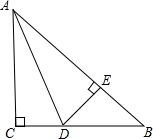 已知:在等腰Rt△ABC中,AC=BC∠C=90°,AD平分∠BAC,DE⊥AB于点E,AB=15cm,
已知:在等腰Rt△ABC中,AC=BC∠C=90°,AD平分∠BAC,DE⊥AB于点E,AB=15cm,