题目内容
为缓解油价上涨给出租车待业带来的成本压力,某巿自2007年11月17日起,调整出租车运价,调整方案见下列表格及图象(其中a,b,c为常数)| 行驶路程 | 收费标准 | |
| 调价前 | 调价后 | |
| 不超过3km的部分 | 起步价6元 | 起步价a 元 |
| 超过3km不超出6km的部分 | 每公里2.1元 | 每公里b元 |
| 超出6km的部分 | 每公里c元 |
①填空:a=______,b=______,c=______.
②写出当x>3时,y1与x的关系,并在上图中画出该函数的图象.
③函数y1与y2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在请说明理由.
【答案】分析:①a由图可直接得出;b、c根据:运价÷路程=单价,代入数值,求出即可;
②当x>3时,y1与x的关系,有两部分组成,第一部分为6,第二部分为(x-3)×2.1,所以,两部分相加,就可得到函数式,并可画出图象;
③当y1=y2时,交点存在,求出x的值,再代入其中一个式子中,就能得到y值;y值的意义就是指运价;
解答: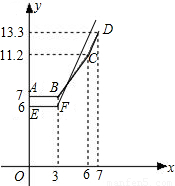 解:①由图可知,a=7元,
解:①由图可知,a=7元,
b=(11.2-7)÷(6-3)=1.4元,
c=(13.3-11.2)÷(7-6)=2.1元;
②由图得,当x>3时,y1与x的关系式是:
y1=6+(x-3)×2.1,
整理得,y1=2.1x-0.3;
③由图得,当3<x<6时,y2与x的关系式是:
y2=7+(x-3)×1.4,
整理得,y2=1.4x+2.8;
所以,当y1=y2时,交点存在,
即,2.1x-0.3=1.4x+2.8,
解得,x=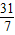 ,y=9;
,y=9;
所以,函数y1与y2的图象存在交点( ,9);
,9);
其意义为:当x<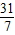 时,是方案调价前合算,当x>
时,是方案调价前合算,当x> 时,方案调价后合算;
时,方案调价后合算;
点评:本题主要考查了一次函数在实际问题中的应用,能够根据题意中的等量关系建立函数关系式;能够根据函数解析式求得对应的x的值;作图关键是确定交点;体现了数形结合思想.
②当x>3时,y1与x的关系,有两部分组成,第一部分为6,第二部分为(x-3)×2.1,所以,两部分相加,就可得到函数式,并可画出图象;
③当y1=y2时,交点存在,求出x的值,再代入其中一个式子中,就能得到y值;y值的意义就是指运价;
解答:
 解:①由图可知,a=7元,
解:①由图可知,a=7元,b=(11.2-7)÷(6-3)=1.4元,
c=(13.3-11.2)÷(7-6)=2.1元;
②由图得,当x>3时,y1与x的关系式是:
y1=6+(x-3)×2.1,
整理得,y1=2.1x-0.3;
③由图得,当3<x<6时,y2与x的关系式是:
y2=7+(x-3)×1.4,
整理得,y2=1.4x+2.8;
所以,当y1=y2时,交点存在,
即,2.1x-0.3=1.4x+2.8,
解得,x=
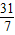 ,y=9;
,y=9;所以,函数y1与y2的图象存在交点(
 ,9);
,9);其意义为:当x<
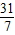 时,是方案调价前合算,当x>
时,是方案调价前合算,当x> 时,方案调价后合算;
时,方案调价后合算;点评:本题主要考查了一次函数在实际问题中的应用,能够根据题意中的等量关系建立函数关系式;能够根据函数解析式求得对应的x的值;作图关键是确定交点;体现了数形结合思想.

练习册系列答案
相关题目
为缓解油价上涨给出租车行业带来的成本压力,某巿自2007年11月17日起,调整出租车运价,调整方案见下列表格及图象(其中a,b,c为常数).
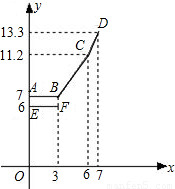
设行驶路程xkm时,调价前的运价y1(元),调价后的运价为y2(元).如图,折线ABCD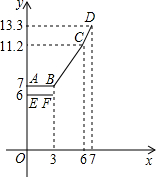 表示y2与x之间的函数关系式,线段EF表示当0≤x≤3时,y1与x的函数关系式,根据图表信息,完成下列各题:
表示y2与x之间的函数关系式,线段EF表示当0≤x≤3时,y1与x的函数关系式,根据图表信息,完成下列各题:
①填空:a= ,b= ,c= ;
②写出当x>3时,y1与x的关系,并在上图中画出该函数的图象;
③函数y1与y2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在,请说明理由.
设行驶路程xkm时,调价前的运价y1(元),调价后的运价为y2(元).如图,折线ABCD
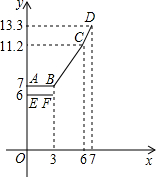 表示y2与x之间的函数关系式,线段EF表示当0≤x≤3时,y1与x的函数关系式,根据图表信息,完成下列各题:
表示y2与x之间的函数关系式,线段EF表示当0≤x≤3时,y1与x的函数关系式,根据图表信息,完成下列各题:| 行驶路程 | 收费标准 | |
| 调价前 | 调价后 | |
| 不超过3km的部分 | 起步价6元 | 起步价a 元 |
| 超过3km不超出6km的部分 | 每公里2.1元 | 每公里b元 |
| 超出6km的部分 | 每公里c元 | |
②写出当x>3时,y1与x的关系,并在上图中画出该函数的图象;
③函数y1与y2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在,请说明理由.
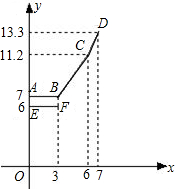 为缓解油价上涨给出租车待业带来的成本压力,某巿自2007年11月17日起,调整出租车运价,调整方案见下列表格及图象(其中a,b,c为常数)
为缓解油价上涨给出租车待业带来的成本压力,某巿自2007年11月17日起,调整出租车运价,调整方案见下列表格及图象(其中a,b,c为常数)| 行驶路程 | 收费标准 | |
| 调价前 | 调价后 | |
| 不超过3km的部分 | 起步价6元 | 起步价a 元 |
| 超过3km不超出6km的部分 | 每公里2.1元 | 每公里b元 |
| 超出6km的部分 | 每公里c元 |
①填空:a=
②写出当x>3时,y1与x的关系,并在上图中画出该函数的图象.
③函数y1与y2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在请说明理由.
为缓解油价上涨给出租车行业带来的成本压力,某巿自2012年5月1日起,调
为缓解油价上涨给出租车行业带来的成本压力,某巿自2012年5月1日起,调整出租车运价,调整方案见下列表格及图像(其中a,b为常数).
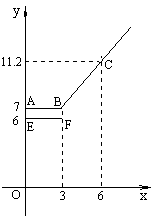
设行驶路程x km时,调价前的运价为y1(元),调价后的运价为y2(元).如图,折线ABC表示y2与x之间的函数关系式,线段EF表示当0≤x≤3时,y1与x的函数关系式,根据图表信息,完成下列各题:
【小题1】填空:a= , b= .
【小题2】写出当x>3时,y1与x的函数关系式,并在上图中画出该函数的图象.
【小题3】函数y1与y2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在,请说明理由.
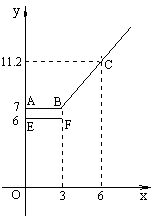
为缓解油价上涨给出租车行业带来的成本压力,某巿自2012年5月1日起,调整出租车运价,调整方案见下列表格及图像(其中a,b为常数).
| 行驶路程 | 收费标准 | |
| 调价前 | 调价后 | |
| 不超过3km的部分 | 起步价6元 | 起步价a元 |
| 超过3km的部分 | 每公里2.1元 | 每公里b元 |
【小题1】填空:a= , b= .
【小题2】写出当x>3时,y1与x的函数关系式,并在上图中画出该函数的图象.
【小题3】函数y1与y2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在,请说明理由.

为缓解油价上涨给出租车行业带来的成本压力,某巿自2012年5月1日起,调
为缓解油价上涨给出租车行业带来的成本压力,某巿自2012年5月1日起,调整出租车运价,调整方案见下列表格及图像(其中a,b为常数).
| 行驶路程 | 收费标准 | |
| 调价前 | 调价后 | |
| 不超过3km的部分 | 起步价6元 | 起步价a元 |
| 超过3km的部分 | 每公里2.1元 | 每公里b元 |
【小题1】填空:a= , b= .
【小题2】写出当x>3时,y1与x的函数关系式,并在上图中画出该函数的图象.
【小题3】函数y1与y2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在,请说明理由.