题目内容
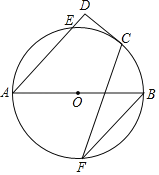
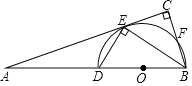
【题目】已知:如图,BD是半圆O的直径,A是BD延长线上的一点,BC⊥AE,交AE的延长线于点C,交半圆O于点F,且E为弧DF的中点.
(1)求证:AC是半圆O的切线;
(2)若BC=8,BE=6![]() ,求半径的长.
,求半径的长.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)要证AC是⊙O的切线,只要连接OE,再证DE⊥AC即可;
(2)根据相似三角形的性质即可求出结论.
(1)证明:连接OE.
∵E为![]() 的中点,
的中点,
∴![]() ,
,
∴∠OBE=∠CBE,
∵OE=OB,
∴∠OEB=∠OBE,
∴∠OEB=∠CBE,
∴OE∥BC,
∵BC⊥AC,
∴∠C=90°,
∴∠AEO=∠C=90°,即OE⊥AC,
又∵OE为半圆O的半径,
∴AC是半圆O的切线;
(2)∵E为![]() 的中点,
的中点,
∴![]() ,
,
∴∠OBE=∠CBE,
∵∠BED=∠C=90°,
∴△BDE∽△BEC,
∴![]() ,
,
∴![]() ,
,
∴BD=9,
∴半径的长为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目