题目内容
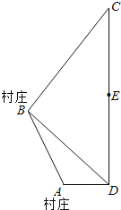
【题目】(1)发现探究:如图1,矩形![]() 和矩形
和矩形![]() 位似,
位似,![]() ,连接
,连接![]() ,则线段
,则线段![]() 与
与![]() 有何数量关系,关系是__________.直线
有何数量关系,关系是__________.直线![]() 与直线
与直线![]() 所夹锐角的度数是__________.
所夹锐角的度数是__________.
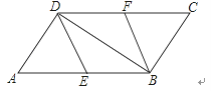
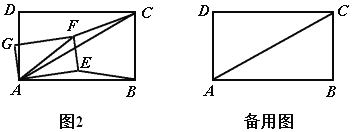
(2)拓展探究:如图2,将矩形![]() 绕点
绕点![]() 逆时针旋转角
逆时针旋转角![]()
![]() ,上面的结论是否仍然成立?如果成立,请就图2给出的情况加以证明.
,上面的结论是否仍然成立?如果成立,请就图2给出的情况加以证明.
(3)问题解决:若点![]() 是
是![]() 的中点,
的中点,![]() ,连接
,连接![]() ,
,![]() ,在矩形
,在矩形![]() 绕点
绕点![]() 旋转过程中,请直接写出
旋转过程中,请直接写出![]() 长的取值范围.
长的取值范围.
【答案】(1)![]() ;
;![]() ;(2)结论仍然成立,详见解析;(3)
;(2)结论仍然成立,详见解析;(3)![]() .
.
【解析】
(1)由矩形的性质和三角函数的知识可得∠BAC=30°,然后根据位似图形的性质可得A、F、C三点共线,EF∥BC以及直线![]() 与直线
与直线![]() 所夹锐角的度数,再根据平行线分线段成比例定理即得
所夹锐角的度数,再根据平行线分线段成比例定理即得![]() 与
与![]() 的数量关系;
的数量关系;
(2)易得![]() ,故可根据两边成比例且夹角相等证明
,故可根据两边成比例且夹角相等证明![]() ∽
∽![]() ,于是可得
,于是可得![]() ,∠ABE=∠ACF,于是只要求出
,∠ABE=∠ACF,于是只要求出![]() 即可求出直线
即可求出直线![]() 与直线
与直线![]() 所夹锐角的度数,进而可得结论;
所夹锐角的度数,进而可得结论;
(3)如图3,取![]() 的中点N,连接GN、MN,由三角形的三边关系可知:
的中点N,连接GN、MN,由三角形的三边关系可知:![]() (“=”号仅当G、N、M三点共线时成立),然后根据三角形的中位线定理和直角三角形斜边中线的性质可分别求出MN和GN的长,进而可得结果.
(“=”号仅当G、N、M三点共线时成立),然后根据三角形的中位线定理和直角三角形斜边中线的性质可分别求出MN和GN的长,进而可得结果.
解:(1)∵![]() ,∠B=90°,
,∠B=90°,
∴∠BAC=30°,
∵矩形![]() 和矩形
和矩形![]() 位似,
位似,
∴A、F、C三点共线,EF∥BC,直线![]() 与直线
与直线![]() 所夹锐角的度数是30°,
所夹锐角的度数是30°,
∴![]() ;
;
故答案为:![]() ;
;![]() ;
;
(2)结论仍然成立.
证明:如图2,
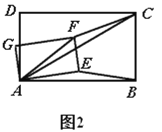
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() ,∠ABE=∠ACF,
,∠ABE=∠ACF,
∴![]() ,
,
∴直线![]() 与直线
与直线![]() 所夹锐角的度数=
所夹锐角的度数=![]() ;
;
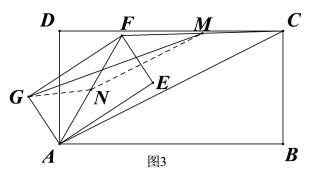
(3)如图3,取![]() 的中点N,连接GN、MN,在
的中点N,连接GN、MN,在![]() 中,
中,![]() (“=”号仅当G、N、M三点共线时成立),
(“=”号仅当G、N、M三点共线时成立),
∵![]() ,∴
,∴![]() ,
,
∵N为AF中点,M为CF中点,
∴![]() ,
,
∵N为AF中点,∠AGF=90°,![]() ,
,
∴![]() ,
,
∴![]()
即GM长的取值范围是:![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】小明为探究函数![]() 的图象和性质,需要画出函数图象,列表如下:
的图象和性质,需要画出函数图象,列表如下:
| …… |
|
|
|
|
|
|
|
|
|
| …… |
| …… |
|
|
|
|
|
|
|
|
|
| …… |
根据上表数据,在平面直角坐标系中描点,画出函数图象,如图如示,小明画出了图象的一部分.
(1)请你帮小明画出完整的![]() 的图象;
的图象;
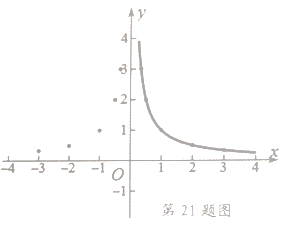
(2)观察函数图象,请写出这个函数的两条性质:
性质一: ;
性质二: .
(3)利用上述图象,探究函数![]() 图象与直线
图象与直线![]() 的关系;
的关系;
①当![]() 时, 直线
时, 直线![]() 与函数
与函数![]() 在第一象限的图象有一个交点
在第一象限的图象有一个交点![]() ,则
,则![]() 的坐标是 ;
的坐标是 ;
②当![]() 为何值时,讨论函数
为何值时,讨论函数![]() 的图象与直线
的图象与直线![]() 的交点个数.
的交点个数.
【题目】新冠肺炎疫情发生后,口罩市场出现热销,小明的爸爸用12000元购进医用外科、N95两种型号的口罩在自家药房销售,销售完后共获利2700元,进价和售价如下表:
品名价格 | 医用外科口罩 | N95口罩 |
进价(元/袋) | 20 | 30 |
售价(元/袋) | 25 | 36 |
(1)小明爸爸的药房购进医用外科、N95两种型号口罩各多少袋?
(2)该药房第二次以原价购进医用外科、N95两种型号口罩,购进医用外科口罩袋数不变,而购进N95口罩袋数是第一次的2倍,医用外科口罩按原售价出售,而效果更好的N95口罩打折让利销售,若两种型号的口罩全部售完,要使第二次销售活动获利不少于2460元,每袋N95口罩最多打几折?
【题目】丁老师为了解所任教的两个班的学生数学学习情况,对数学进行了一次测试,获得了两个班的成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.
①A、B两班学生(两个班的人数相同)数学成绩不完整的频数分布直方图如下(数据分成5组:x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100):
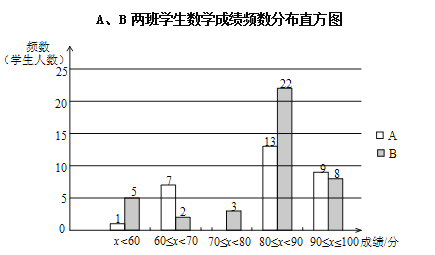
②A、B两班学生测试成绩在80≤x<90这一组的数据如下:
A班:80 80 82 83 85 85 86 87 87 87 88 89 89
B班:80 80 81 81 82 82 83 84 84 85 85 86 86 86 87 87 87 87 87 88 88 89
③A、B两班学生测试成绩的平均数、中位数、方差如下:
平均数 | 中位数 | 方差 | |
A班 | 80.6 | m | 96.9 |
B班 | 80.8 | n | 153.3 |
根据以上信息,回答下列问题:
(1)补全数学成绩频数分布直方图;
(2)写出表中m、n的值;
(3)请你对比分析A、B两班学生的数学学习情况(至少从两个不同的角度分析).