题目内容
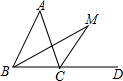 如图,已知:BM是△ABC的∠ABC的平分线,CM是∠ACD的平分线,如果∠A=50°,则∠M等于( )
如图,已知:BM是△ABC的∠ABC的平分线,CM是∠ACD的平分线,如果∠A=50°,则∠M等于( )分析:先根据三角形内角和定理及∠A=58°求出∠ABC+∠ACB的度数,再根据角平分线的定义及三角形外角的性质用∠A、∠ABC、∠ACB表示出∠BCM及∠MBC的度数,再利用三角形内角和定理即可求出∠M的度数.
解答:解:∵∠A=50°,∴∠ABC+∠ACB=180°-∠A=180°-50°=130°…①,
∵BM是∠ABC的平分线,∴∠MBC=
∠ABC,
∵∠ACD是△ABC的外角,CM是外角∠ACD的角平分线,
∴∠ACM=
(∠A+∠ABC),
∴∠BCM=∠ACB+∠ACM=∠ACB+
(∠A+∠ABC),
∵∠M+∠MBC+∠ACB+∠ACH=180°,
∴∠M+
∠ABC+∠ACB+
(∠A+∠ABC)=180°,即∠M+(∠ABC+∠ACB)+
∠A=180°…②,
把①代入②得,∠M+130°+
×50°=180°,
∴∠M=25°.
故选A.
∵BM是∠ABC的平分线,∴∠MBC=
| 1 |
| 2 |
∵∠ACD是△ABC的外角,CM是外角∠ACD的角平分线,
∴∠ACM=
| 1 |
| 2 |
∴∠BCM=∠ACB+∠ACM=∠ACB+
| 1 |
| 2 |
∵∠M+∠MBC+∠ACB+∠ACH=180°,
∴∠M+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
把①代入②得,∠M+130°+
| 1 |
| 2 |
∴∠M=25°.
故选A.
点评:本题考查的是三角形内角和定理、三角形内角及外角平分线的性质,解答此题的关键是熟知以下知识:
(1)三角形内角和为180°;
(2)三角形的外角等于不相邻的两个内角的和.
(1)三角形内角和为180°;
(2)三角形的外角等于不相邻的两个内角的和.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
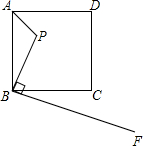 如图,已知点P是边长为5的正方形ABCD内一点,且PB=3,BF⊥BP于B,若在射线BF上找一点M,使以点B,M,C为顶点的三角形与△ABP相似,BM的值为( )
如图,已知点P是边长为5的正方形ABCD内一点,且PB=3,BF⊥BP于B,若在射线BF上找一点M,使以点B,M,C为顶点的三角形与△ABP相似,BM的值为( )| A、3 | ||
B、
| ||
C、3或
| ||
| D、3或5 |
 如图,已知四边形ABCD是矩形,且MO=MD=4,MC=3.
如图,已知四边形ABCD是矩形,且MO=MD=4,MC=3. 20、如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形.
20、如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形. 如图,已知:BM是△ABC的∠ABC的平分线,CM是∠ACD的平分线,如果∠A=50°,则∠M等于
如图,已知:BM是△ABC的∠ABC的平分线,CM是∠ACD的平分线,如果∠A=50°,则∠M等于