题目内容
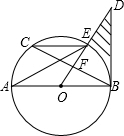 如图,已知AB是⊙O的直径,点E是弧BC的中点,DE与BC交于点F,∠CEA=∠ODB.
如图,已知AB是⊙O的直径,点E是弧BC的中点,DE与BC交于点F,∠CEA=∠ODB.(1)请判断直线BD与⊙O的位置关系,并给出证明;
(2)当AB=12,BF=3
| 3 |
| 3 |
考点:切线的判定,扇形面积的计算
专题:
分析:(1)要证直线BD和⊙O相切,通过∠BOD=∠BAC,因为∠BAC+∠ABC=90°,所以证明OB⊥BD即可;
(2)S阴影=S△OBD-S扇形OBE.
(2)S阴影=S△OBD-S扇形OBE.
解答:(1)解法一:直线BD与⊙O相切.
证明如下:
∵∠AEC=∠ODB,∠AEC=∠ABC,
∴∠ABC=∠ODB.
∵点E是弧BC的中点,
∴OD⊥BC,
∴∠DBC+∠ODB=90°,
∴∠ABD=∠ABC+∠DBC=∠DBC+∠ODB=90°,
∴直线BD与⊙O相切;
解法二:直线BD与⊙O相切.
证明如下:如图,连接AC.
∵AB是⊙O的直径,
∴∠ACB=90°.
∵点E是弧BC的中点,
∴OD⊥BC,
∴∠OFB=90°=∠ACB,
∴AC∥OD,
∴∠CAB=∠DOB.
∵∠CEA=∠ODB=∠ABC,
∴∠CAB+∠CBA=∠DOB+∠ODB=90°,
∴∠DBO=90°,
∴直线BD与⊙O相切;
(2)解:∵点E是弧BC的中点,
∴OD⊥BC,
∴∠OFB=90°.
∵BO=
AB=6,
∴sin∠DOB=
=
=
,
∴∠DOB=60°.
∵∠OBD=90°,
∴tan60°=
=
=
,
∴BD=6
,
∴S=
-
=18
-6π≈18×1.73-6×3.14≈12.
证明如下:
∵∠AEC=∠ODB,∠AEC=∠ABC,
∴∠ABC=∠ODB.
∵点E是弧BC的中点,
∴OD⊥BC,
∴∠DBC+∠ODB=90°,
∴∠ABD=∠ABC+∠DBC=∠DBC+∠ODB=90°,
∴直线BD与⊙O相切;
解法二:直线BD与⊙O相切.
证明如下:如图,连接AC.
∵AB是⊙O的直径,
∴∠ACB=90°.
∵点E是弧BC的中点,
∴OD⊥BC,
∴∠OFB=90°=∠ACB,

∴AC∥OD,
∴∠CAB=∠DOB.
∵∠CEA=∠ODB=∠ABC,
∴∠CAB+∠CBA=∠DOB+∠ODB=90°,
∴∠DBO=90°,
∴直线BD与⊙O相切;
(2)解:∵点E是弧BC的中点,
∴OD⊥BC,
∴∠OFB=90°.
∵BO=
| 1 |
| 2 |
∴sin∠DOB=
| BF |
| BO |
3
| ||
| 6 |
| ||
| 2 |
∴∠DOB=60°.
∵∠OBD=90°,
∴tan60°=
| BD |
| OB |
| BD |
| 6 |
| 3 |
∴BD=6
| 3 |
∴S=
6×6
| ||
| 2 |
| 60π×62 |
| 360 |
| 3 |
点评:本题考查了扇形的面积计算,切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,点A、D、B、E在一直线上,AD=BE,AC=DF,AC∥DF.
如图,点A、D、B、E在一直线上,AD=BE,AC=DF,AC∥DF. 在△ABC中,∠BAC=90°,AD⊥BC于D,CF是∠ACB的平分线,交AD于E,交AB于F,求证:∠AEF=∠AFE.
在△ABC中,∠BAC=90°,AD⊥BC于D,CF是∠ACB的平分线,交AD于E,交AB于F,求证:∠AEF=∠AFE.