题目内容
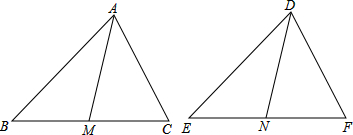
 如图,点A、D、B、E在一直线上,AD=BE,AC=DF,AC∥DF.
如图,点A、D、B、E在一直线上,AD=BE,AC=DF,AC∥DF.(1)四边形BEFC是平行四边形吗?
(2)与∠E相等的角有哪些?请说明理由(不再添加其它字母与线段).
考点:平行四边形的判定与性质
专题:
分析:(1)首先由“由一组对边平行且相等”推知四边形ACFD是平行四边形,则根据“平行四边形的对边平行,且相等”证得CF∥AD,CF=AD,所以结合已知条件易得CF∥BE,CF=BE,所以四边形BEFC是平行四边形;
(2)由平行四边形的对角相等和对边平行,以及平行线的性质来解题.
(2)由平行四边形的对角相等和对边平行,以及平行线的性质来解题.
解答:解:(1)四边形BEFC是平行四边形.理由如下:
如图,∵AC=DF,AC∥DF,
∴四边形ACFD是平行四边形,
∴CF∥AD,CF=AD.
又∵点A、D、B、E在一直线上,AD=BE,
∴CF∥BE,CF=BE,
∴四边形BEFC是平行四边形;
(2)与∠E相等的角有∠FCB,∠ABC.理由如下:
∵由(1)知,四边形BEFC是平行四边形,
∴∠E=∠FCB,CB∥FE,
∴∠E=∠ABC.
如图,∵AC=DF,AC∥DF,
∴四边形ACFD是平行四边形,
∴CF∥AD,CF=AD.
又∵点A、D、B、E在一直线上,AD=BE,
∴CF∥BE,CF=BE,
∴四边形BEFC是平行四边形;
(2)与∠E相等的角有∠FCB,∠ABC.理由如下:
∵由(1)知,四边形BEFC是平行四边形,
∴∠E=∠FCB,CB∥FE,
∴∠E=∠ABC.
点评:本题考查了平行四边形的判定与性质.平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.

练习册系列答案
相关题目
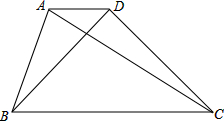 如图,已知梯形ABCD中,AD∥CB,AD=1,BC=4,BD=3,AC=4,求梯形ABCD面积.
如图,已知梯形ABCD中,AD∥CB,AD=1,BC=4,BD=3,AC=4,求梯形ABCD面积.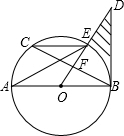 如图,已知AB是⊙O的直径,点E是弧BC的中点,DE与BC交于点F,∠CEA=∠ODB.
如图,已知AB是⊙O的直径,点E是弧BC的中点,DE与BC交于点F,∠CEA=∠ODB.